题目内容
5.已知α是第二象限角,且sinα=$\frac{3}{5}$,f(x)=sin2αcosx+cos2αsinx的图象关于直线x=x0对称,则tanx0=( )| A. | -$\frac{7}{24}$ | B. | $\frac{7}{24}$ | C. | -$\frac{3}{4}$ | D. | $\frac{3}{4}$ |
分析 利用两角和的正弦化简,再由f(x)的图象关于直线x=x0对称得到${x}_{0}=kπ+\frac{π}{2}-2α,k∈Z$.则tanx0=$\frac{1}{tan2α}$.由已知求得tanα后代入二倍角的正切公式得答案.
解答 解:∵f(x)=sin2αcosx+cos2αsinx=sin(x+2α)的图象关于直线x=x0对称,
∴${x}_{0}+2α=kπ+\frac{π}{2}$,${x}_{0}=kπ+\frac{π}{2}-2α,k∈Z$.
∴tanx0=tan($kπ+\frac{π}{2}-2α$)=$\frac{1}{tan2α}$.
∵α是第二象限角,且sinα=$\frac{3}{5}$,∴cosα=-$\frac{4}{5}$,tanα=$-\frac{3}{4}$.
则tanx0=$\frac{1}{tan2α}$=$\frac{1-ta{n}^{2}α}{2tanα}$=$\frac{1-(-\frac{3}{4})^{2}}{2×(-\frac{3}{4})}=-\frac{7}{24}$.
故选:A.
点评 本题考查三角函数中的恒等变换应用,考查了三角函数的图象和性质,属中档题.

练习册系列答案
相关题目
15.已知x1,x2,…x9组成公差为1的等差数列,随机变量X所有取值为x1,x2,…x9,且等可能地取每一个值,则X的方差为( )
| A. | $\frac{20}{3}$ | B. | $\frac{10}{3}$ | C. | 60 | D. | 30 |
16.若θ是两条异面直线所成的角,则( )
| A. | θ∈(0,π] | B. | $θ∈(0,\frac{π}{2}]$ | C. | $θ∈[0,\frac{π}{2}]$ | D. | $θ∈(0,\frac{π}{2})$ |
15.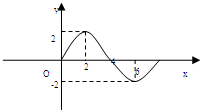 函数f(x)=Acos(ωx+ϕ)(A>0,ω>0)的部分图象如图所示,则f(1)+f(2)+…+f(2011)+f(2012)的值为( )
函数f(x)=Acos(ωx+ϕ)(A>0,ω>0)的部分图象如图所示,则f(1)+f(2)+…+f(2011)+f(2012)的值为( )
 函数f(x)=Acos(ωx+ϕ)(A>0,ω>0)的部分图象如图所示,则f(1)+f(2)+…+f(2011)+f(2012)的值为( )
函数f(x)=Acos(ωx+ϕ)(A>0,ω>0)的部分图象如图所示,则f(1)+f(2)+…+f(2011)+f(2012)的值为( )| A. | 2+$\sqrt{2}$ | B. | $\sqrt{2}$ | C. | $2+2\sqrt{2}$ | D. | 0 |