题目内容
15.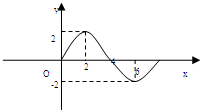 函数f(x)=Acos(ωx+ϕ)(A>0,ω>0)的部分图象如图所示,则f(1)+f(2)+…+f(2011)+f(2012)的值为( )
函数f(x)=Acos(ωx+ϕ)(A>0,ω>0)的部分图象如图所示,则f(1)+f(2)+…+f(2011)+f(2012)的值为( )| A. | 2+$\sqrt{2}$ | B. | $\sqrt{2}$ | C. | $2+2\sqrt{2}$ | D. | 0 |
分析 根函数f(x)=Acos(ωx+φ)(A>0,ω>0)及其图象,可以求得A=2,ω=$\frac{π}{4}$,利用函数的周期性可以求得答案.
解答 解:由图象知A=2,T=$\frac{2π}{ω}=8$可得ω=$\frac{π}{4}$,
由五点对应法得$\frac{π}{4}×2+φ=0$,可求得$φ=-\frac{π}{2}$,
∴$f(x)=2sin\frac{π}{4}x$,
又f(1)+f(2)+f(3)+…+f(8)=0,
∴f(1)+f(2)+f(3)+…+f(2012)=f(1)+f(2)+f(3)+f(4)=2sin$\frac{π}{4}$+2sin$\frac{π}{2}$+2sin$\frac{3π}{4}$+2sinπ=2×$\frac{\sqrt{2}}{2}$+2+2×$\frac{\sqrt{2}}{2}$
=2+2$\sqrt{2}$,
故选:C.
点评 本题考查三角函数解析式的求解,根据三角函数的图象与周期性是解决本题的关键.,难点在于根据图象求得A,ω,φ的值,属于中档题.

练习册系列答案
 夺冠训练单元期末冲刺100分系列答案
夺冠训练单元期末冲刺100分系列答案 新思维小冠军100分作业本系列答案
新思维小冠军100分作业本系列答案 名师指导一卷通系列答案
名师指导一卷通系列答案
相关题目
5.已知α是第二象限角,且sinα=$\frac{3}{5}$,f(x)=sin2αcosx+cos2αsinx的图象关于直线x=x0对称,则tanx0=( )
| A. | -$\frac{7}{24}$ | B. | $\frac{7}{24}$ | C. | -$\frac{3}{4}$ | D. | $\frac{3}{4}$ |
3.如图,D,E,F分别是△ABC的边AB,BC,CA的中点,则( )
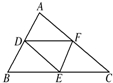

| A. | $\overrightarrow{AD}+\overrightarrow{BE}+\overrightarrow{CF}=\overrightarrow{0}$ | B. | $\overrightarrow{BD}-\overrightarrow{CF}+\overrightarrow{DF}=\overrightarrow{0}$ | C. | $\overrightarrow{AD}+\overrightarrow{CE}-\overrightarrow{CF}=\overrightarrow{0}$ | D. | $\overrightarrow{BD}-\overrightarrow{BE}-\overrightarrow{FC}=\overrightarrow{0}$ |
10.在复平面内,复数z=-2-3i对应的点位于( )
| A. | 第一象限 | B. | 第二象限 | C. | 第三象限 | D. | 第四象限 |
20.已知函数f(x)=$\sqrt{{x}^{2}-1}$.若f(a)=2$\sqrt{2}$,则实数a=( )
| A. | $\sqrt{3}$ | B. | -3 | C. | 3或-3 | D. | $\sqrt{3}$或-$\sqrt{3}$ |
4.已知(2x+$\frac{a}{x}$)5的展开式中各项系数之和为1,则该展开式中含$\frac{1}{{x}^{3}}$项系数为( )
| A. | -20 | B. | 20 | C. | -10 | D. | 10 |