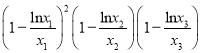Question

【题目】下列命题中，正确的序号是 ． ①y=﹣2cos（ π﹣2x）是奇函数；
②若α，β是第一象限角，且α＞β，则sinα＞sinβ；
③x=﹣ 是函数y=3sin（2x﹣ ）的一条对称轴；
④函数y=sin（ ﹣2x）的单调减区间是[kπ﹣ ，kπ+ ]（k∈Z）

Answer 1

【答案】①③④
【解析】解：对于①，y=﹣2cos（ π﹣2x）=2sin2x，是定义域R上的奇函数，命题正确； 对于②，α，β是第一象限角，且α=390°＞β=30°，则sinα=sinβ，原命题错误；
对于③，x=﹣ 时，函数y=3sin（2x﹣ ）=3sin（2×（﹣ ）﹣ ）=3取得最大值，
∴x=﹣ 是函数y=3sin（2x﹣ ）的一条对称轴，命题正确；
对于④，函数y=sin（ ﹣2x）=﹣sin（2x﹣ ），
令﹣ +2kπ≤2x﹣ ≤ +2kπ，k∈Z，
解得﹣ +kπ≤x≤ +kπ，k∈Z，
∴y=sin（ ﹣2x）的单调减区间是[kπ﹣ ，kπ+ ]（k∈Z），命题正确；
综上，正确的命题序号是①③④．
所以答案是：①③④．