题目内容
7.如图,⊙O直径AB=2r,弦CD=r,点E是CD的中点.CF⊥AB于F,连接EF,则∠CFE=30°.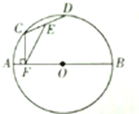
分析 如图,连接OE、OC.利用垂径定理和30度角所对的直角边为斜边的一半得到∠COE=30°;然后由“对角互补的四边形为圆内接四边形”得到四边形CDFE四点共圆,则同弧所对的圆周角相等:∠CFE=∠COE=30°.
解答 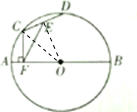 解:如图,连接OE、OC.
解:如图,连接OE、OC.
∵O是圆心,点E是CD的中点,
∴OE⊥CD.
又∵⊙O直径AB=2r,弦CD=r,
∴OC=2CE,
∴∠COE=30°.
又∵CF⊥AB,
∴∠CFO+∠CEO=180°,
∴四边形COFE四点共圆,
∴∠CFE=∠COE=30°.
故答案是:30°.
点评 本题考查了圆内接多边形的性质与判定.解答该题的难点是由“对角互补的四边形为圆内接四边形”推知四边形CDFE四点共圆.

练习册系列答案
 学练快车道快乐假期寒假作业系列答案
学练快车道快乐假期寒假作业系列答案
相关题目
1. 在如图所示的方框中,每个方框涂一种颜色,且相邻的方框涂不同的颜色,现有3种不同的颜色可供选择,则不同的涂色方案共有( )
在如图所示的方框中,每个方框涂一种颜色,且相邻的方框涂不同的颜色,现有3种不同的颜色可供选择,则不同的涂色方案共有( )
 在如图所示的方框中,每个方框涂一种颜色,且相邻的方框涂不同的颜色,现有3种不同的颜色可供选择,则不同的涂色方案共有( )
在如图所示的方框中,每个方框涂一种颜色,且相邻的方框涂不同的颜色,现有3种不同的颜色可供选择,则不同的涂色方案共有( )| A. | 12种 | B. | 16种 | C. | 18种 | D. | 24种 |
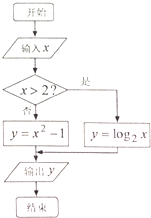 某函数的解析式由如图所示的程序框图给出.
某函数的解析式由如图所示的程序框图给出.