题目内容
【题目】已知函数![]() ,其中
,其中![]() 为自然对数底数.
为自然对数底数.
(1)当![]() 时,求函数
时,求函数![]() 在点
在点![]() 处的切线方程;
处的切线方程;
(2)讨论函数![]() 的单调性,并写出相应的单调区间;
的单调性,并写出相应的单调区间;
(3)已知![]() ,若函数
,若函数![]() 对任意
对任意![]() 都成立,求
都成立,求![]() 的最大值.
的最大值.
【答案】(1)![]() (2)当
(2)当![]() 时,函数
时,函数![]() 的单调递增区间为
的单调递增区间为![]() ;当
;当![]() 时,函数
时,函数![]() 的单调递增区间为
的单调递增区间为![]() ,单调递减区间为
,单调递减区间为![]() .(3)
.(3)![]()
【解析】
试题分析:(1)根据导数几何意义可求切线斜率:![]() ,再根据点斜式求切线方程为
,再根据点斜式求切线方程为![]() ,即
,即![]() .(2)利用导数求函数单调性,从导函数出发,研究其零点情况:
.(2)利用导数求函数单调性,从导函数出发,研究其零点情况:![]() 当
当![]() 时,
时,![]() ,无零点,函数
,无零点,函数![]() 在
在![]() 上单调递增;当
上单调递增;当![]() 时,由
时,由![]() 得
得![]() ,
,![]() 时,
时,![]() ,
,![]() 单调递减;
单调递减;![]() 时,
时,![]() ,
,![]() 单调递增.(3)不等式恒成立问题转化为函数最值问题:
单调递增.(3)不等式恒成立问题转化为函数最值问题:![]() ,当
,当![]() 时,函数
时,函数![]() 无最小值;当
无最小值;当![]() 时,函数
时,函数![]() 最小值为0,
最小值为0,![]() ,此时
,此时![]() ;当
;当![]() 时,
时,![]() ,
,![]() ,
,![]() ,最后研究函数
,最后研究函数![]() 最大值
最大值![]()
试题解析:解:(1)当![]() 时,
时,![]() ,
,![]() ,
,![]() , 2分
, 2分
∴函数![]() 在点
在点![]() 处的切线方程为
处的切线方程为![]() ,
,
即![]() . 4分
. 4分
(2)∵![]() ,
,
①当![]() 时,
时,![]() ,函数
,函数![]() 在
在![]() 上单调递增; 6分
上单调递增; 6分
②当![]() 时,由
时,由![]() 得
得![]() ,
,
∴![]() 时,
时,![]() ,
,![]() 单调递减;
单调递减;![]() 时,
时,![]() ,
,![]() 单调递增.
单调递增.
综上,当![]() 时,函数
时,函数![]() 的单调递增区间为
的单调递增区间为![]() ;当
;当![]() 时,函数
时,函数![]() 的单调递增区间为
的单调递增区间为![]() ,单调递减区间为
,单调递减区间为![]() . 9分
. 9分
(3)由(2)知,当![]() 时,函数
时,函数![]() 在
在![]() 上单调递增,
上单调递增,
∴![]() 不可能恒成立; 10分
不可能恒成立; 10分
当![]() 时,
时,![]() ,此时
,此时![]() ; 11分
; 11分
当![]() 时,由函数
时,由函数![]() 对任意
对任意![]() 都成立,得
都成立,得![]() ,
,
∵![]() ,∴
,∴![]() 13分
13分
∴![]() ,
,
设![]() ,∴
,∴ ![]() ,
,
由于![]() ,令
,令![]() ,得
,得![]() ,
,![]() ,
,
当 时,
时,![]() ,
,![]() 单调递增;
单调递增;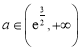 时,
时,![]() ,
,![]() 单调递减.
单调递减.
∴![]() ,即
,即![]() 的最大值为
的最大值为![]() ,
,
此时![]() . 16分
. 16分

练习册系列答案
相关题目