题目内容
已知 ,
,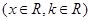
(1)若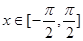 ,且
,且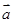 ∥(
∥(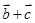 ),求x的值;
),求x的值;
(2)若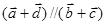 ,求实数
,求实数 的取值范围.
的取值范围.
(1) 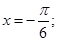 (2)
(2) 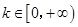 .
.
解析试题分析:(1)先将向量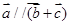 化为代数式,即
化为代数式,即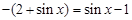 ,
,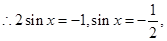
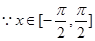 ;
;
(2)由已知先写出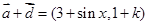 ,
,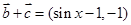 的坐标,再由
的坐标,再由 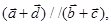 则有:
则有: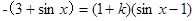 当
当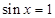 时等式不成立;将
时等式不成立;将 写成关于
写成关于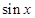 的函数,即
的函数,即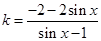 ,再求函数的值域即是
,再求函数的值域即是 的取值范围为
的取值范围为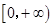
(或解)用 表示
表示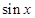 ,即
,即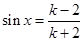 ,又因为
,又因为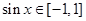 ,可解
,可解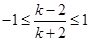 得
得 的取值范围为
的取值范围为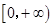 .
.
试题解析:(1)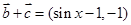 ,
,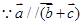 ,
, 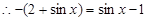 ,
,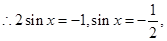
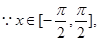
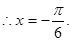
(2)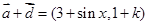 ,
,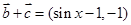
若 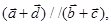 则有:
则有: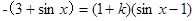
当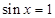 时等式不成立;
时等式不成立;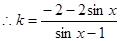 解得:
解得: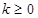
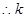 的取值范围为
的取值范围为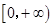
考点:本题考查向量的坐标运算;向量共线的;利用三角函数的有界性求参数.

练习册系列答案
相关题目
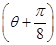 =
=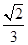 ,求tan θ的值.
,求tan θ的值.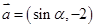 与
与 ,其中
,其中 .
.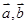 能平行吗?请说明理由;
能平行吗?请说明理由;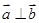 ,求
,求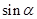 和
和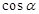 的值;
的值;
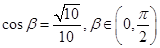 ,求
,求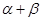 的值.
的值.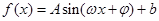 (
(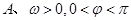 ,
,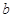 为常数)一段图像如图所示.
为常数)一段图像如图所示.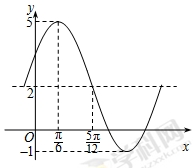
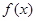 的解析式;
的解析式;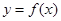 的图像向左平移
的图像向左平移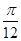 个单位,再将所得图像上各点的横坐标扩大为原来的4倍,得到函数
个单位,再将所得图像上各点的横坐标扩大为原来的4倍,得到函数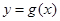 的图像,求函数
的图像,求函数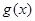 的单调递增区间.
的单调递增区间.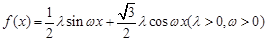 的部分图象如图所示,其中点为最高点,点为图象与轴的交点,在
的部分图象如图所示,其中点为最高点,点为图象与轴的交点,在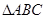 中,角
中,角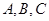 对边为
对边为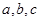 ,
,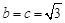 ,且满足
,且满足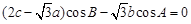 .
.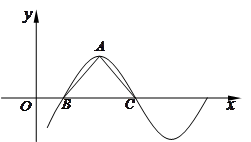
 的单调递增区间.
的单调递增区间. 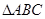 中,角
中,角 、
、 、
、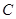 的对边分别为
的对边分别为 、
、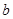 、
、 ,且
,且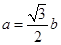 ,
,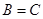 .
.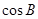 的值;
的值; ,求
,求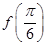 的值.
的值.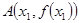 ,
,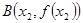 是函数
是函数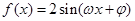
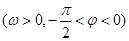 图象上的任意两点,且角
图象上的任意两点,且角 的终边经过点
的终边经过点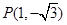 ,若
,若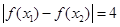 时,
时,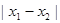 的最小值为
的最小值为 .
. 的解析式;
的解析式;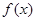 的单调递增区间;
的单调递增区间;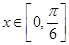 时,不等式
时,不等式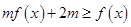 恒成立,求实数
恒成立,求实数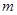 的取值范围.
的取值范围.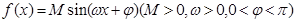 在一个周期上的系列对应值如下表:
在一个周期上的系列对应值如下表: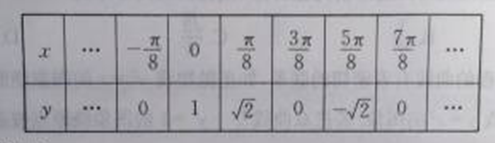
 的表达式;
的表达式; 的三个内角
的三个内角 、
、 、
、 所对的边分别为
所对的边分别为 、
、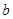 、
、 ,且满足
,且满足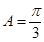 ,
,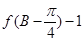 ,
,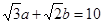 ,求边长
,求边长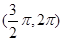 ,且a⊥b.
,且a⊥b.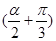 的值.
的值.