题目内容
已知函数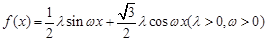 的部分图象如图所示,其中点为最高点,点为图象与轴的交点,在
的部分图象如图所示,其中点为最高点,点为图象与轴的交点,在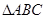 中,角
中,角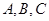 对边为
对边为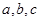 ,
,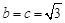 ,且满足
,且满足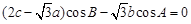 .
.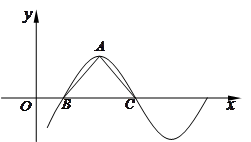
(Ⅰ)求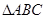 的面积;
的面积;
(Ⅱ)求函数 的单调递增区间.
的单调递增区间.
(Ⅰ)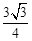 ;(Ⅱ)
;(Ⅱ)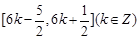 ;
;
解析试题分析:(Ⅰ)由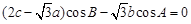 ,根据正弦定理得
,根据正弦定理得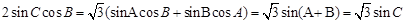 ,得
,得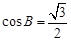 得
得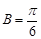 ,则
,则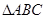 中,
中, 边上的高
边上的高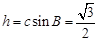 ,故
,故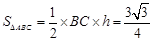 ;(Ⅱ)对
;(Ⅱ)对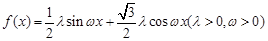 化简得
化简得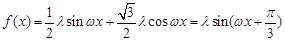 又
又 长度为半个周期长,根据
长度为半个周期长,根据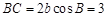 ,则
,则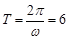 得
得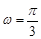 ,故
,故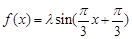 ,根据正弦函数的单调性得
,根据正弦函数的单调性得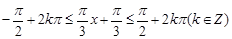 ,化简求出函数
,化简求出函数 的单调递增区间为
的单调递增区间为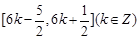 .
.
试题解析:(Ⅰ)由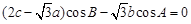 ,得
,得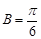 3分
3分
在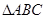 中,
中, 边上的高
边上的高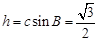 ,故
,故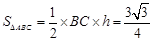 6分
6分
(Ⅱ)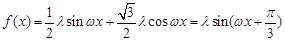 ,
,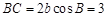
又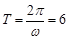 ,则
,则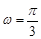 ,故
,故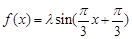 9分
9分
又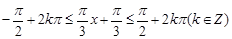 ,可得
,可得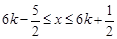
所以函数 的单调递增区间为
的单调递增区间为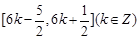 .. 12分.
.. 12分.
考点:1.正弦定理应用;2.解三角形;3. 函数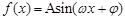 的应用.
的应用.

练习册系列答案
相关题目
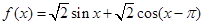 .
.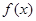 的最小正周期和值域;
的最小正周期和值域;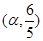 ,
,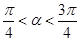 .求
.求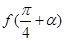 的值.
的值.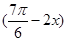 +2cos2x-1(x∈R).
+2cos2x-1(x∈R). ,b,a,c成等差数列,且
,b,a,c成等差数列,且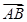 ·
·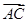 =9,求a的值.
=9,求a的值.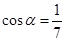 ,
,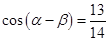 ,且
,且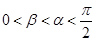 ,求
,求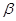 的值;
的值;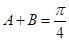 ,求证:
,求证: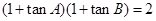 .
. ,
,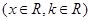
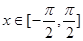 ,且
,且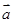 ∥(
∥(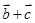 ),求x的值;
),求x的值;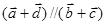 ,求实数
,求实数 的取值范围.
的取值范围.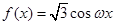 ,
,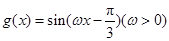 ,且
,且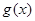 的最小正周期为
的最小正周期为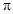 .
.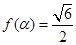 ,
,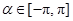 ,求
,求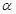 的值;
的值;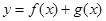 的单调增区间.
的单调增区间.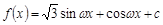 (
(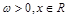 ,c是实数常数)的图像上的一个最高点
,c是实数常数)的图像上的一个最高点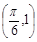 ,与该最高点最近的一个最低点是
,与该最高点最近的一个最低点是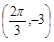 ,
,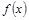 的解析式及其单调增区间;
的解析式及其单调增区间;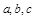 ,且
,且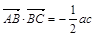 ,角A的取值范围是区间M,当
,角A的取值范围是区间M,当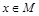 时,试求函数
时,试求函数 .
.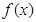 的最小正周期;
的最小正周期; 个单位,得到函数
个单位,得到函数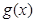 的图象,求函数
的图象,求函数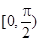 上的最大值和最小值,并求出相应的x的值.
上的最大值和最小值,并求出相应的x的值. .
.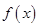 的单调递减区间及最小正周期;
的单调递减区间及最小正周期;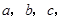 若
若 ,
,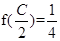 ,求
,求