题目内容
已知向量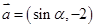 与
与 ,其中
,其中 .
.
(1)问向量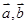 能平行吗?请说明理由;
能平行吗?请说明理由;
(2)若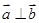 ,求
,求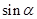 和
和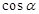 的值;
的值;
(3)在(2)的条件下,若
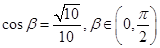 ,求
,求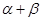 的值.
的值.
(1)不能平行;(2)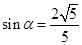 ,
,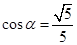 ;(3)
;(3)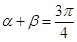 .
.
解析试题分析:(1)先假设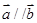 ,列方程得
,列方程得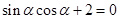 ,然后利用正弦的二倍角公式化简得
,然后利用正弦的二倍角公式化简得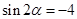 ,再判断此方程是否有解,若有解,可判断
,再判断此方程是否有解,若有解,可判断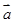 、
、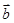 可能平行;若无解,则可判断
可能平行;若无解,则可判断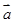 、
、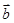 不可能平行;(2)将向量的垂直问题转化为向量的数量积问题,得到
不可能平行;(2)将向量的垂直问题转化为向量的数量积问题,得到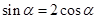 ,联立方程
,联立方程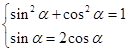 ,并结合
,并结合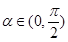 ,即可求出
,即可求出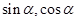 ;(3)先由同角三角函数的基本关系式计算出
;(3)先由同角三角函数的基本关系式计算出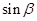 ,然后再根据两角和的余弦公式展开计算得
,然后再根据两角和的余弦公式展开计算得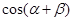 的值,最后结合
的值,最后结合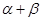 的取值范围确定
的取值范围确定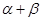 的值即可.
的值即可.
试题解析:解:(1)向量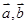 不能平行
不能平行
若平行,需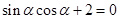 ,即
,即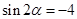 ,而
,而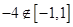
则向量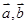 不能平行 4分
不能平行 4分
(2)因为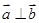 ,所以
,所以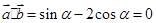 5分
5分
即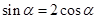
又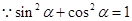 6分
6分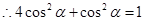 ,即
,即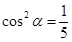 ,
,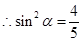
又
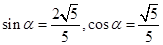 8分
8分
(3)由(2)知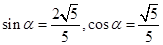
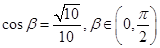 ,得
,得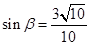 9分
9分
则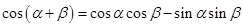
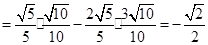 11分
11分
又 ,则
,则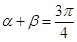 12分.
12分.
考点:1.向量平行、垂直的判定与应用;2.同角三角函数的基本关系式;3.两角和与差的三角函数.

练习册系列答案
 捷径训练检测卷系列答案
捷径训练检测卷系列答案 小夫子全能检测系列答案
小夫子全能检测系列答案
相关题目
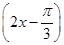 +2sin2x,x∈R.
+2sin2x,x∈R.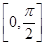 时,求函数f(x)的最大值和最小值及相应的x值.
时,求函数f(x)的最大值和最小值及相应的x值. 的图象与y轴的交点为
的图象与y轴的交点为 ,它在y轴右侧的第一个最高点和第一个最低点的坐标分别为
,它在y轴右侧的第一个最高点和第一个最低点的坐标分别为

 的解析式及
的解析式及 的值;
的值; 满足
满足 的值.
的值.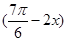 +2cos2x-1(x∈R).
+2cos2x-1(x∈R). ,b,a,c成等差数列,且
,b,a,c成等差数列,且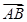 ·
·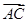 =9,求a的值.
=9,求a的值.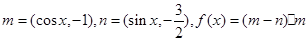 .
.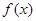 的单调增区间;
的单调增区间;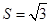 ,
,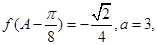 求b+c的值.
求b+c的值.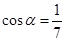 ,
,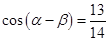 ,且
,且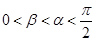 ,求
,求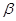 的值;
的值;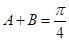 ,求证:
,求证: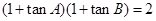 .
. ,
,
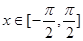 ,且
,且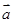 ∥(
∥(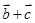 ),求x的值;
),求x的值;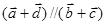 ,求实数
,求实数 的取值范围.
的取值范围.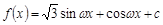 (
(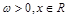 ,c是实数常数)的图像上的一个最高点
,c是实数常数)的图像上的一个最高点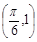 ,与该最高点最近的一个最低点是
,与该最高点最近的一个最低点是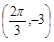 ,
,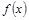 的解析式及其单调增区间;
的解析式及其单调增区间;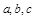 ,且
,且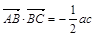 ,角A的取值范围是区间M,当
,角A的取值范围是区间M,当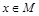 时,试求函数
时,试求函数 的最大值为2,周期为
的最大值为2,周期为 .
. 的解析式,并由此求出函数的单调增区间;
的解析式,并由此求出函数的单调增区间;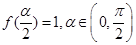 ,求
,求 的值.
的值.