题目内容
【题目】已知椭圆 ![]() =1的一个焦点为F(2,0),且离心率为
=1的一个焦点为F(2,0),且离心率为 ![]()
(1)求椭圆方程;
(2)过点M(3,0)作直线与椭圆交于A,B两点,求△OAB面积的最大值.
【答案】
(1)解:依题意有c=2, ![]() =
= ![]() ,又a2=b2+c2,
,又a2=b2+c2,
可得a2=6,b2=2.
故椭圆方程为 ![]() =1.
=1.
(2)解:由题意可知过点M的直线斜率存在且不等于0,设直线方程为y=k(x﹣3).
联立方程组 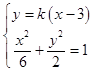 ,消去x得(1+3k2)y2+6ky+3k2=0,
,消去x得(1+3k2)y2+6ky+3k2=0,
∴y1+y2=﹣ ![]() ,y1y2=
,y1y2= ![]() ,
,
∴S△OAB= ![]() |OM||y1﹣y2|=
|OM||y1﹣y2|= ![]() ×3×
×3× ![]()
= ![]() 3
3 ![]() =3
=3 ![]() =3
=3 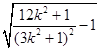 ,
,
令3k2+1=t≥1,则S△OAB=3 ![]() =3
=3 ![]() ≤
≤ ![]() ,当且仅当t=
,当且仅当t= ![]() ,即k2=
,即k2= ![]() ,k=
,k= ![]() 时取等号.
时取等号.
∴△OAB面积的最大值为 ![]() .
.
【解析】(1)依题意有c=2, ![]() =
= ![]() ,又a2=b2+c2,联立解出即可得出.(2)由题意可知过点M的直线斜率存在且不等于0,设直线方程为y=k(x﹣3).与椭圆方程联立可得(1+3k2)y2+6ky+3k2=0,利用根与系数的关系可得:S△OAB=
,又a2=b2+c2,联立解出即可得出.(2)由题意可知过点M的直线斜率存在且不等于0,设直线方程为y=k(x﹣3).与椭圆方程联立可得(1+3k2)y2+6ky+3k2=0,利用根与系数的关系可得:S△OAB= ![]() |OM||y1﹣2|=3
|OM||y1﹣2|=3 ![]() =3
=3 ![]() ,令3k2+1=t≥1,可得S△OAB=3
,令3k2+1=t≥1,可得S△OAB=3 ![]() =3
=3 ![]() ,利用二次函数的单调性即可得出.
,利用二次函数的单调性即可得出.

【题目】某商场举行优惠促销活动,顾客仅可以从以下两种优惠方案中选择一种, 方案一:每满200元减50元:
方案二:每满200元可抽奖一次.具体规则是依次从装有3个红球、1个白球的甲箱,装有2个红球、2个白球的乙箱,以及装有1个红球、3个白球的丙箱中各随机摸出1个球,所得结果和享受的优惠如下表:(注:所有小球仅颜色有区别)
红球个数 | 3 | 2 | 1 | 0 |
实际付款 | 半价 | 7折 | 8折 | 原价 |
(Ⅰ)若两个顾客都选择方案二,各抽奖一次,求至少一个人获得半价优惠的概率;
(Ⅱ)若某顾客购物金额为320元,用所学概率知识比较哪一种方案更划算?