题目内容
【题目】某校举行运动会,其中三级跳远的成绩在8.0米(四舍五入,精确到0.1米)以上的进入决赛,把所得数据进行整理后,分成6组画出频率分布直方图的一部分(如图),已知从左到右前5个小组的频率分别为0.04,0.10,0.14,0.28,0.30,第6小组的频数是7.
(Ⅰ)求进入决赛的人数;
(Ⅱ)若从该校学生(人数很多)中随机抽取两名,记X表示两人中进入决赛的人数,求X的分布列及数学期望;
(Ⅲ)经过多次测试后发现,甲成绩均匀分布在8~10米之间,乙成绩均匀分布在9.5~10.5米之间,现甲,乙各跳一次,求甲比乙远的概率.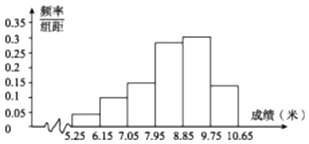
【答案】(Ⅰ)解:第6小组的频率为1﹣(0.04+0.10+0.14+0.28+0.30)=0.14,
∴总人数为 ![]() (人).
(人).
∴第4、5、6组成绩均进入决赛,人数为(0.28+0.30+0.14)×50=36(人)
即进入决赛的人数为36.
(Ⅱ)由题意知X的可能取值为0,1,2,进入决赛的概率为 ![]() ,
,
∴X~ ![]() ,
, ![]() ,
,
P(X=1)= ![]() ,
,
![]() .
.
∴所求分布列为:
X | 0 | 1 | 2 |
P |
|
|
|
![]() ,两人中进入决赛的人数的数学期望为
,两人中进入决赛的人数的数学期望为 ![]() .
.
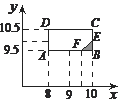
(Ⅲ)设甲、乙各跳一次的成绩分别为x、y米,
则基本事件满足的区域为: ![]() ,
,
事件A“甲比乙远的概率”满足的区域为x>y,如图所示.
∴由几何概型P(A)= ![]() =
= ![]() .
.
即甲比乙远的概率为 ![]() .
.
【解析】(Ⅰ)由频率分直方图求出第6小组的频率,从而求出总人数,进而得到第4、5、6组成绩均进入决赛,由此能求出进入决赛的人数.
(Ⅱ)由题意知X的可能取值为0,1,2,进入决赛的概率为 ![]() ,从而X~
,从而X~ ![]() ,由此能求出X的分布列及数学期望.
,由此能求出X的分布列及数学期望.
(Ⅲ)设甲、乙各跳一次的成绩分别为x、y米,则基本事件满足的区域为: ![]() ,由此利用几何概型能求出甲比乙远的概率.
,由此利用几何概型能求出甲比乙远的概率.
【考点精析】根据题目的已知条件,利用频率分布直方图的相关知识可以得到问题的答案,需要掌握频率分布表和频率分布直方图,是对相同数据的两种不同表达方式.用紧凑的表格改变数据的排列方式和构成形式,可展示数据的分布情况.通过作图既可以从数据中提取信息,又可以利用图形传递信息.

 一诺书业暑假作业快乐假期云南美术出版社系列答案
一诺书业暑假作业快乐假期云南美术出版社系列答案