题目内容
【题目】已知函数f(x)=axln(x+1)+x+1(x>﹣1,a∈R).
(1)若 ![]() ,求函数f(x)的单调区间;
,求函数f(x)的单调区间;
(2)当x≥0时,不等式f(x)≤ex恒成立,求实数a的取值范围.
【答案】
(1)解:a= ![]() 时,f(x)=
时,f(x)= ![]() xln(x+1)+x+1,
xln(x+1)+x+1,
f′(x)= ![]() [ln(x+1)+1﹣
[ln(x+1)+1﹣ ![]() ]+1,
]+1,
∵f′(x)在(﹣1,+∞)递增,且f′(﹣1+ ![]() )=0,
)=0,
故x∈(﹣1,﹣1+ ![]() )时,f′(x)<0,f(x)递减,
)时,f′(x)<0,f(x)递减,
x∈(﹣1+ ![]() ,+∞)时,f′(x)>0,f(x)递减,
,+∞)时,f′(x)>0,f(x)递减,
故f(x)在(﹣1,﹣1+ ![]() )递减,在(﹣1+
)递减,在(﹣1+ ![]() ,+∞);
,+∞);
(2)解:记g(x)=f(x)﹣ex(x≥0),g(0)=0,
则g′(x)=a[ln(x+1)+1﹣ ![]() ]+1﹣ex,
]+1﹣ex,
记h(x)=a[ln(x+1)+1﹣ ![]() ]+1﹣ex,
]+1﹣ex,
h′(x)=a[ 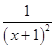 +
+ ![]() ]﹣ex,h′(0)=2a﹣1,
]﹣ex,h′(0)=2a﹣1,
①a≤ ![]() 时,∵
时,∵ 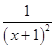 +
+ ![]() ∈(0,2],ex≥1,
∈(0,2],ex≥1,
∴h′(x)≤0,h(x)在(0,+∞)递减,
则h(x)≤h(0)=0,即g′(x)≤0,∴g(x)在(0,+∞)递减,
∴g(x)≤g(0)=0恒成立,即f(x)≤ex恒成立,满足题意;
②a≥ ![]() 时,h′(x)在(0,+∞)递减,
时,h′(x)在(0,+∞)递减,
又h′(0)=2a﹣1>0,x→+∞时,h′(x)→﹣∞,
则必存在x0∈(0,+∞),使得h′(x0)=0,
则x∈(0,x0)时,h′(x)>0,h(x)在(0,x0)递增,
此时h(x)>h(0)=0,
x∈(0,x0)时,g′(x)>0,∴g(x)在(0,x0)递增,
∴g(x)>g(0)=0,即f(x)>ex,不合题意,
综上,a≤ ![]() .
.
【解析】(1)求出函数的导数,解关于导函数的不等式,求出函数的单调区间即可;(2)记g(x)=f(x)﹣ex(x≥0),g(0)=0,求出函数的导数,记h(x)=a[ln(x+1)+1﹣ ![]() ]+1﹣ex,通过讨论a的范围,求出函数的单调性,从而确定a的具体范围即可.
]+1﹣ex,通过讨论a的范围,求出函数的单调性,从而确定a的具体范围即可.

 期末好成绩系列答案
期末好成绩系列答案 99加1领先期末特训卷系列答案
99加1领先期末特训卷系列答案