Question

【题目】已知集合A={（x，y）|（x﹣3﹣4cosq）2+（y﹣5﹣4sinq）2=4，θ∈R}，B={（x，y）|3x+4y﹣19=0}.记集合P=A∩B，则集合P所表示的轨迹的长度为( )

A.8B.8C.8D.8

Answer 1

【答案】A

【解析】

由圆（x﹣3﹣4cosq）2+（y﹣5﹣4sinq）2=4的圆心为（3+4cosq，5+4sinq），可知其圆心的轨迹方程为（x﹣3）2+（y﹣5）2=16，易知动圆（x﹣3﹣4cosq）2+（y﹣5﹣4sinq）2=4所形成的图形为圆环，利用垂径定理结合图像，即可得解.

集合A={（x，y）|（x﹣3﹣4cosq）2+（y﹣5﹣4sinq）2=4，θ∈R}，

圆的圆心（3+4cosq，5+4sinq），半径为2，

所以圆的圆心的轨迹方程为：（x﹣3）2+（y﹣5）2=16，

如图：

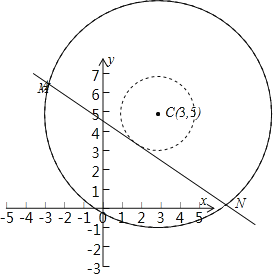
集合A的图形是图形中两个圆中间的圆环部分，

圆心C（3，5）到直线3x+4y﹣19=0的距离为：d2，

所以，A∩B就是|MN|=228.

故选：A.