题目内容
【题目】设有限数列![]() ,定义集合
,定义集合![]() 为数列
为数列![]() 的伴随集合.
的伴随集合.
(Ⅰ)已知有限数列![]() 和数列
和数列![]() .分别写出
.分别写出![]() 和
和![]() 的伴随集合;
的伴随集合;
(Ⅱ)已知有限等比数列![]() ,求
,求![]() 的伴随集合
的伴随集合![]() 中各元素之和
中各元素之和![]() ;
;
(Ⅲ)已知有限等差数列![]() ,判断
,判断![]() 是否能同时属于
是否能同时属于![]() 的伴随集合
的伴随集合![]() ,并说明理由.
,并说明理由.
【答案】(Ⅰ)数列![]() 的伴随集合为
的伴随集合为![]() ,数列
,数列![]() 的伴随集合为
的伴随集合为![]() ;(Ⅱ)
;(Ⅱ)![]() (Ⅲ)不能
(Ⅲ)不能
【解析】
(Ⅰ)由数列A的伴随集合定义可得P,Q的伴随集合;
(Ⅱ)先证明对任意i≠k或j≠l,则ai+aj≠ak+al(1≤i<j≤n,1≤k<l≤n),可得求集合M中各元素之和时,每个ai(1≤i≤n)均出现n﹣1次,由等比数列的求和公式,计算可得所求和;
(Ⅲ)假设![]() 同时属于数列A的伴随集合M.设数列A的公差为d(d≠0),运用等差数列的定义和通项公式、性质,推理论证得到矛盾,即可判断.
同时属于数列A的伴随集合M.设数列A的公差为d(d≠0),运用等差数列的定义和通项公式、性质,推理论证得到矛盾,即可判断.
解:(Ⅰ)数列![]() 的伴随集合为
的伴随集合为![]() ,数列
,数列![]() 的伴随集合为
的伴随集合为![]() .
.
(Ⅱ)先证明对任意![]() 或
或![]() ,则
,则![]() .
.
假设![]() .
.
当![]() 且
且![]() ,因为
,因为![]() ,则
,则![]() ,即
,即![]() ,
,
所以![]() ,与
,与![]() 矛盾.
矛盾.
同理,当![]() 且
且![]() 时,也不成立.
时,也不成立.
当![]() 且
且![]() 时,不妨设
时,不妨设![]() ,因为
,因为![]() ,则
,则![]() ,
,
所以![]() ,
,
左边为奇数,右边为偶数,所以![]() ,
,
综上,对任意![]() 或
或![]() ,则
,则![]()
所以求集合![]() 中各元素之和时,每个
中各元素之和时,每个![]() 均出现
均出现![]() 次,
次,
所以![]()
![]()
(Ⅲ)假设![]() 同时属于数列
同时属于数列![]() 的伴随集合
的伴随集合![]() .
.
设数列![]() 的公差为
的公差为![]() ,则
,则
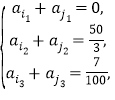 即
即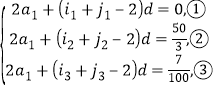
②-①得,![]() ,
,
③-①得,![]() ,
,
两式相除得,![]() ,
,
因为![]() ,
,
所以![]() ,
,
![]() ,
,
所以![]() .
.
又因为![]() ,
,
所以![]() ,
,
![]() ,
,
所以![]() ,与
,与![]() 矛盾,
矛盾,
所以![]() 不能同时属于数列
不能同时属于数列![]() 的伴随集合
的伴随集合![]() .
.

练习册系列答案
相关题目