题目内容
【题目】如图,矩形
和梯形
所在平面互相垂直，
，
,
,
，
，
.
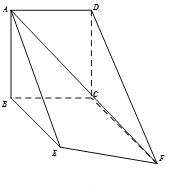
（1）求证：
//平面
；
（2）当
的长为何值时，二面角
的大小为
.
【答案】（1）见解析；（2）
【解析】
(1)建立空间直角坐标系，由平面向量的法向量证明线面平行即可；
(2)分别求得半平面的法向量，由二面角的余弦值公式得到关于AB长度的方程，解方程即可确定AB的长.
面
面BEFC，
面ABCD，且
，
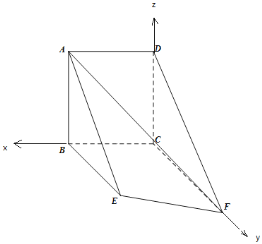
面BEFC．
以点C为坐标原点，以CB，CF和CD分别作为x轴，y轴和z轴，建立空间直角坐标系
．
设
，则
0，
，
，
0，，
，
4，，
0，
，
，
，
，
所以
，
，
又
所以
平面CDF．
即
为平面CDF的法向量
又
，
，又
平面CDF
所以
平面
设
与平面AEF垂直，则，
，
由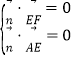
，得
，解得
又因为
平面BEFC，
，
所以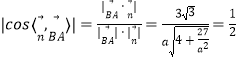
，
得到
．
所以当
时，二面角
的大小为
练习册系列答案
各地期末复习特训卷系列答案
小博士期末闯关100分系列答案
相关题目
