题目内容
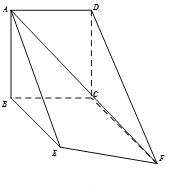
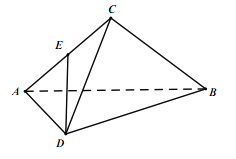
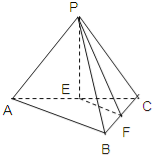
【题目】如图,在三棱锥P﹣ABC中,E,F分别为AC,BC的中点.
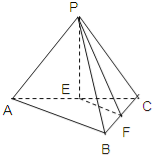
(1)求证:EF∥平面PAB;
(2)若平面PAC⊥平面ABC,且PA=PC,∠ABC=90°,求证:平面PEF⊥平面PBC.
【答案】见解析
【解析】
试题(1)利用E,F分别是AC,BC的中点,说明EF∥AB,通过直线与平面平行的判定定理直接证明EF∥平面PAB.
(2)证明PE⊥AC,利用平面与平面垂直的判定定理证明PE⊥平面ABC,通过证明PE⊥BC.EF⊥BC,EF∩PE=E,证明BC⊥平面PEF,然后推出平面PEF⊥平面PBC.
证明:(1)∵E,F分别是AC,BC的中点,∴EF∥AB.
又EF平面PAB,
AB平面PAB,
∴EF∥平面PAB.
(2)在三角形PAC中,∵PA=PC,E为AC中点,
∴PE⊥AC.
∵平面PAC⊥平面ABC,
平面PAC∩平面ABC=AC,
∴PE⊥平面ABC.
∴PE⊥BC.
又EF∥AB,∠ABC=90°,∴EF⊥BC,
又EF∩PE=E,
∴BC⊥平面PEF.
∴平面PEF⊥平面PBC.

【题目】某公司生产一种产品,从流水线上随机抽取100件产品,统计其质量指数并绘制频率分布直方图(如图1):
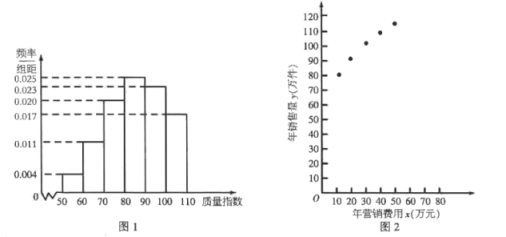
产品的质量指数在![]() 的为三等品,在
的为三等品,在![]() 的为二等品,在
的为二等品,在![]() 的为一等品,该产品的三、二、一等品的销售利润分别为每件1.5,3.5,5.5(单位:元),以这100件产品的质量指数位于各区间的频率代替产品的质量指数位于该区间的概率.
的为一等品,该产品的三、二、一等品的销售利润分别为每件1.5,3.5,5.5(单位:元),以这100件产品的质量指数位于各区间的频率代替产品的质量指数位于该区间的概率.
(1)求每件产品的平均销售利润;
(2)该公司为了解年营销费用![]() (单位:万元)对年销售量
(单位:万元)对年销售量![]() (单位:万件)的影响,对近5年的年营销费用
(单位:万件)的影响,对近5年的年营销费用![]() 和年销售量
和年销售量![]()
![]() 数据做了初步处理,得到的散点图(如图2)及一些统计量的值.
数据做了初步处理,得到的散点图(如图2)及一些统计量的值.
|
|
|
|
16.30 | 24.87 | 0.41 | 1.64 |
表中![]() ,
,![]() ,
,![]() ,
,![]()
根据散点图判断,![]() 可以作为年销售量
可以作为年销售量![]() (万件)关于年营销费用
(万件)关于年营销费用![]() (万元)的回归方程.
(万元)的回归方程.
(ⅰ)建立![]() 关于
关于![]() 的回归方程;
的回归方程;
(ⅱ)用所求的回归方程估计该公司应投入多少营销费,才能使得该产品一年的收益达到最大?(收益=销售利润-营销费用,取![]() )
)
参考公式:对于一组数据:![]() ,
,![]() ,
,![]() ,
,![]() ,其回归直线
,其回归直线![]() 的斜率和截距的最小乘估计分别为
的斜率和截距的最小乘估计分别为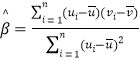 ,
,![]()
【题目】某品牌经销商在一广场随机采访男性和女性用户各50名,其中每天玩微信超过6小时的用户列为“微信控”,否则称其为“非微信控”,调查结果如下:
微信控 | 非微信控 | 合计 | |
男性 | 26 | 24 | 50 |
女性 | 30 | 20 | 50 |
合计 | 56 | 44 | 100 |
(1)根据以上数据,能否有95%的把握认为“微信控”与“性别”有关?
(2)现从调查的女性用户中按分层抽样的方法选出5人,求所抽取的5人中“微信控”和“非微信控”的人数;
(3)从(2)中抽取的5位女性中,再随机抽取3人赠送礼品,试求抽取3人中恰有2人位“微信控”的概率.
参考公式: 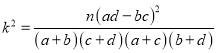 ,其中
,其中![]() .
.
参考数据:
| 0.50 | 0.40 | 0.25 | 0.15 | 0.10 | 0.05 | 0.025 |
| 0.455 | 0.708 | 1.323 | 2.072 | 2.706 | 3.841 | 5.024 |