Question

【题目】已知椭圆C的中心在原点，焦点在x轴上，左、右焦点分别为F1、F2，且|F1F2|＝2，点在椭圆C上．

(1)求椭圆C的方程；

(2)过F1的直线l与椭圆C相交于A、B两点，且△AF2B的面积为，求直线l的方程．

Answer 1

【答案】（1）；（2）y=±(x+1).

【解析】试题分析：（1）根据椭圆定义求得2a，再根据焦距得c，解得b（2）先设直线方程，根据点到直线距离得高，联立直线方程与椭圆方程，利用韦达定理与弦长公式得底，最后代入三角形面积公式得k

试题解析：(1)设椭圆的方程为 (a>b>0)，由题意可得椭圆C两焦点坐标分别为F1(－1,0)，F2(1,0)．

∴2a＝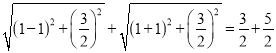

＝4.∴a＝2，又c＝1，∴b2＝4－1＝3，

故椭圆C的方程为

(2)当直线l⊥x轴时，计算得到：A，B，S△AF2B＝·|AB|·|F1F2|＝×3×2＝3，不符合题意．

当直线l与x轴不垂直时，设直线l的方程为：y＝k(x＋1)，代入

消去y得(3＋4k2)x2＋8k2x＋4k2－12＝0.

显然Δ>0成立，设A(x1，y1)，B(x2，y2)，

则x1＋x2＝－，x1·x2＝.

又|AB|·

＝·＝ ，

点F2到AB的距离d＝＝，

所以S△AF2B＝|AB|·d＝··＝＝，

化简，得17k4＋k2－18＝0，即(k2－1)(17k2＋18)＝0，解得k＝±1.

所以y=±(x+1).