题目内容
3.已知函数y=x3在x=ak时的切线和x轴交于ak+1,若a1=1,则数列{an}的前n项和为( )| A. | $\frac{1}{3}+\frac{2}{3}n$ | B. | ${(\frac{2}{3})^{n-1}}$ | C. | $3-{(\frac{2}{3})^n}$ | D. | $3-\frac{2^n}{{{3^{n-1}}}}$ |
分析 通过斜率公式计算可得递推关系,进而可得结论.
解答 解:∵函数y=x3,∴y′=3x2,
∴$\frac{{{a}_{k}}^{3}-0}{{a}_{k}-{a}_{k+1}}$=3${{a}_{k}}^{2}$,即$\frac{{a}_{k}}{{a}_{k}-{a}_{k+1}}$=3,
化简得:3ak+1=2ak,即$\frac{{a}_{k+1}}{{a}_{k}}$=$\frac{2}{3}$,
又∵a1=1,∴Sn=$\frac{1-(\frac{2}{3})^{n}}{1-\frac{2}{3}}$=3-$\frac{{2}^{n}}{{3}^{n-1}}$,
故选:D.
点评 本题考查求数列的和,考查运算求解能力,利用斜率求出递推关系是解决本题的关键,注意解题方法的积累,属于中档题.

练习册系列答案
相关题目
18.已知抛物线y2=4x,过其焦点F作倾斜角为$\frac{π}{4}$的直线l,若l与抛物线交于B、C两点,则弦BC的长为( )
| A. | $\frac{10}{3}$ | B. | 2 | C. | 4 | D. | 8 |
8.一位母亲在孩子的成长档案中记录了年龄和身高间的数据(截取其中部分):
根据以上样本数据,建立了身高y(cm)与年龄x(周岁)的线性回归方程为$\widehat{y}$=7.19x+a,可预测该孩子10周岁时的身高为( )
| 年龄(周岁) | 3 | 4 | 5 | 6 | 7 | 8 | 9 |
| 身高 | 94.8 | 104.2 | 108.7 | 117.8 | 124.3 | 130.8 | 139.1 |
| A. | 142.8cm | B. | 145.9cm | C. | 149.8cm | D. | 151.7cm |
15.执行如图所示的程序框图,输出的结果是( )
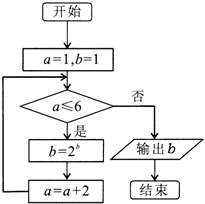

| A. | 4 | B. | 8 | C. | 16 | D. | 216 |
12.复数z=$\frac{2i}{i-1}$+i3(i为虚数单位)的共轭复数为( )
| A. | 1+2i | B. | i-1 | C. | 1-i | D. | 1-2i |
13.已知偶函数f(x)满足当x>0时,3f(x)-2f($\frac{1}{x}$)=$\frac{x}{x+1}$,则f(-2)等于( )
| A. | $\frac{8}{13}$ | B. | $\frac{4}{3}$ | C. | $\frac{4}{15}$ | D. | $\frac{8}{15}$ |
 如图,四棱锥P-ABCD的底面ABCD是平行四边形,M,N分别为PB,CD的中点,二面角P-CD-A的大小为60°,AC=AD=$\sqrt{2}$,CD=PN=2,PC=PD.
如图,四棱锥P-ABCD的底面ABCD是平行四边形,M,N分别为PB,CD的中点,二面角P-CD-A的大小为60°,AC=AD=$\sqrt{2}$,CD=PN=2,PC=PD.