题目内容
8．一位母亲在孩子的成长档案中记录了年龄和身高间的数据（截取其中部分）：| 年龄（周岁） | 3 | 4 | 5 | 6 | 7 | 8 | 9 |
| 身高 | 94.8 | 104.2 | 108.7 | 117.8 | 124.3 | 130.8 | 139.1 |
| A． | 142.8cm | B． | 145.9cm | C． | 149.8cm | D． | 151.7cm |
分析 先计算该组数据的样本中心点坐标，代入回归直线方程，求出a值，进而将x=10代入，可得答案．
解答 解：由已知可得：$\overline{x}$=$\frac{1}{7}$（3+4+5+6+7+8+9）=6，
$\overline{y}$=$\frac{1}{7}$（94.8+104.2+108.7+117.8+124.3+130.8+139.1）=117.1，
将（6，117.1）代入$\widehat{y}$=7.19x+a得：a=73.96，
故$\widehat{y}$=7.19x+73.96，
当x=10时，$\widehat{y}$=71.9+73.96=145.86≈145.9，
故选：B
点评 本题考查的知识点是线性回归方程，熟练掌握线性回归方程必过数据样本中心点，是解答的关键．
练习册系列答案
阅读快车系列答案
相关题目
已知椭圆$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1（a＞b＞0）的一个焦点为F（1，0），且过点（-1，$\frac{3}{2}$），右顶点为A，经过点F的动直线l与椭圆交于B，C两点．
16．下列说法正确的是（ ）
| A． | “若$x=\frac{π}{3}$，则$sinx=\frac{{\sqrt{3}}}{2}$”的逆命题为真 | |
| B． | a，b，c为实数，若a＞b，则ac2＞bc2 | |
| C． | 命题p：?x∈R，使得x2+x-1＜0，则?p：?x∈R，使得x2+x-1＞0 | |
| D． | 若命题?p∧q为真，则p假q真 |
3．已知函数y=x3在x=ak时的切线和x轴交于ak+1，若a1=1，则数列{an}的前n项和为（ ）
| A． | $\frac{1}{3}+\frac{2}{3}n$ | B． | ${（\frac{2}{3}）^{n-1}}$ | C． | $3-{（\frac{2}{3}）^n}$ | D． | $3-\frac{2^n}{{{3^{n-1}}}}$ |
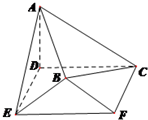如图，在空间几何体ABCDEF中，底面CDEF为矩形，DE=1，CD=2，AD⊥底面CDEF，AD=1，平面BEF⊥底面CDEF，且BE=BF=$\sqrt{2}$．