题目内容
18．已知抛物线y2=4x，过其焦点F作倾斜角为$\frac{π}{4}$的直线l，若l与抛物线交于B、C两点，则弦BC的长为（ ）| A． | $\frac{10}{3}$ | B． | 2 | C． | 4 | D． | 8 |
分析 先根据题意给出直线l的方程，代入抛物线，求出两交点的横坐标的和，然后利用焦半径公式求解即可．
解答 解：由y2=4x得焦点为F（1，0），所以直线l：y=x-1，
代入抛物线y2=4x化简得x2-6x+1=0，
设C（x1，y1），B（x2，y2），则x1+x2=6，
所以|CB|=x1+x2+p=6+2=8．
故所求的弦长为8．
故选：D．
点评 本题考查了直线与抛物线的位置关系中的弦长问题，因为是过焦点的弦长问题，所以利用了焦半径公式．属于基础题．
练习册系列答案
优百分课时互动系列答案
相关题目
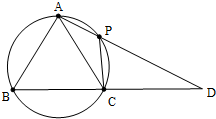在△ABC中，AB=AC，过点A的直线与其外接圆交于点P，交BC延长线于点D．
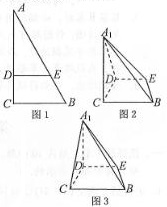如图1，在Rt△ACB中，∠C=90°，BC=3，AC=6，D，E分别是AC，AB上的点，且DE∥BC，DE=2，将△ADE沿DE折起到△A1DE的位置．
3．已知函数y=x3在x=ak时的切线和x轴交于ak+1，若a1=1，则数列{an}的前n项和为（ ）
| A． | $\frac{1}{3}+\frac{2}{3}n$ | B． | ${（\frac{2}{3}）^{n-1}}$ | C． | $3-{（\frac{2}{3}）^n}$ | D． | $3-\frac{2^n}{{{3^{n-1}}}}$ |