题目内容
13．在边长为2的正方形ABCD内部任取一点M，则满足∠AMB＜90°的概率为$1-\frac{π}{8}$．分析 利用已知条件推出满足题目条件的图形面积，利用几何概型求解即可．
解答 解：在边长为2的正方形ABCD内部任取一点M，则满足∠AMB＞90°的M所在区域如图阴影部分，是以1为半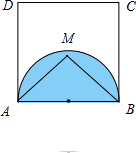
径的半圆以及内部部分，满足几何概型，$\frac{\frac{1}{2}×{1}^{2}π}{4}$=$\frac{π}{8}$
∠AMB＜90°的概率为：$1-\frac{π}{8}$．
故答案为：$1-\frac{π}{8}$．
点评 本题考查几何概型的求法，考查计算能力．
练习册系列答案
优等生题库系列答案
53天天练系列答案
相关题目
已知椭圆$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1（a＞b＞0）的一个焦点为F（1，0），且过点（-1，$\frac{3}{2}$），右顶点为A，经过点F的动直线l与椭圆交于B，C两点．
5．设△ABC的内角A，B，C所对边的长分别为a，b，c，若a=1，c=4$\sqrt{2}$且△ABC的面积为2，则sinC=（ ）
| A． | $\frac{4}{41}$ | B． | $\frac{4}{5}$ | C． | $\frac{4}{25}$ | D． | $\frac{4\sqrt{41}}{41}$ |
2．设Sn为等比数列{an}的前n项和，8a1-a4=0，则$\frac{S_4}{S_2}$=（ ）
| A． | -8 | B． | 8 | C． | 5 | D． | 15 |
3．已知函数y=x3在x=ak时的切线和x轴交于ak+1，若a1=1，则数列{an}的前n项和为（ ）
| A． | $\frac{1}{3}+\frac{2}{3}n$ | B． | ${（\frac{2}{3}）^{n-1}}$ | C． | $3-{（\frac{2}{3}）^n}$ | D． | $3-\frac{2^n}{{{3^{n-1}}}}$ |