题目内容
11.已知函数f(x)=2sinx(sinx+cosx),x∈R.(Ⅰ)求函数f(x)的最小正周期及单调增区间;
(Ⅱ)在△ABC中,角A,B,C所对的边分别为a,b,c,且满足f($\frac{A}{2}$+$\frac{3}{8}$π)=$\frac{2+\sqrt{2}}{2}$,cosC+(cosA-$\sqrt{3}$sinA)cosB=0,a=2$\sqrt{2}$,求△ABC的面积.
分析 (Ⅰ)由三角函数中的恒等变换应用化简函数解析式可得f(x)=$\sqrt{2}$sin(2x-$\frac{π}{4}$)+1,利用正弦函数的周期性和单调性即可得解;
(Ⅱ)已知等式根据三角函数中的恒等变换应用化简可得tanB=$\sqrt{3}$,结合B∈(0,π)可求B,又化简f($\frac{A}{2}+\frac{3π}{8}$)=$\frac{2+\sqrt{2}}{2}$,可得△ABC为正三角形,结合a及三角形面积公式即可得解.
解答 本小题满分为12分
解:(Ⅰ)∵f(x)=2sinx(sinx+cosx)=2sin2x+2sinxcosx=1-cos2x+sin2x=$\sqrt{2}$sin(2x-$\frac{π}{4}$)+1,
∴函数f(x)的最小正周期为π…3分
由2kπ-$\frac{π}{2}$≤2x-$\frac{π}{4}$≤2k$π+\frac{π}{2}$(k∈Z)可得:kπ$-\frac{π}{8}≤x≤$kπ+$\frac{3π}{8}$(k∈Z),
∴函数f(x)的单调增区间为:[kπ$-\frac{π}{8}$,kπ+$\frac{3π}{8}$](k∈Z)…6分
(Ⅱ)在△ABC中,cosC=-cos(A+B),及cosC+(cosA-$\sqrt{3}$sinA)cosB=0,可得:sinAsinB-$\sqrt{3}$sinAcosB=0,而sinA≠0,
∴tanB=$\sqrt{3}$,∵B∈(0,π),∴B=$\frac{π}{3}$.
又∵f($\frac{A}{2}+\frac{3π}{8}$)=$\sqrt{2}$sin(A+$\frac{π}{2}$)+1=$\sqrt{2}$cosA+1=$\frac{2+\sqrt{2}}{2}$,
∴cosA=$\frac{1}{2}$,∴A=$\frac{π}{3}$.
∴△ABC为正三角形,又a=2$\sqrt{2}$,
∴△ABC的面积S=$\frac{\sqrt{3}}{4}×(2\sqrt{2})^{2}$=2$\sqrt{3}$…12分
点评 本题主要考查了三角函数中的恒等变换应用,正弦函数的图象和性质,三角形面积公式的应用,属于基本知识的考查.

| A. | -8 | B. | 8 | C. | 5 | D. | 15 |
| A. | “若$x=\frac{π}{3}$,则$sinx=\frac{{\sqrt{3}}}{2}$”的逆命题为真 | |
| B. | a,b,c为实数,若a>b,则ac2>bc2 | |
| C. | 命题p:?x∈R,使得x2+x-1<0,则?p:?x∈R,使得x2+x-1>0 | |
| D. | 若命题?p∧q为真,则p假q真 |
| A. | $\frac{1}{3}+\frac{2}{3}n$ | B. | ${(\frac{2}{3})^{n-1}}$ | C. | $3-{(\frac{2}{3})^n}$ | D. | $3-\frac{2^n}{{{3^{n-1}}}}$ |
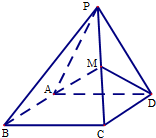 如图,四棱锥P-ABCD,侧面PAD是边长为2的正三角形,且与底面垂直,底面ABCD是∠ABC=60°的菱形,M为棱PC上的动点,且$\frac{PM}{PC}$=λ(λ∈[0,1]).
如图,四棱锥P-ABCD,侧面PAD是边长为2的正三角形,且与底面垂直,底面ABCD是∠ABC=60°的菱形,M为棱PC上的动点,且$\frac{PM}{PC}$=λ(λ∈[0,1]).