题目内容
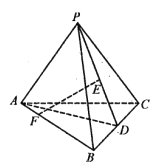
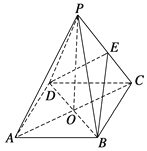
【题目】如图所示,ABCD是正方形,O是正方形的中心,PO⊥底面ABCD,底面边长为a,E是PC的中点.
(1)求证:平面PAC⊥平面BDE;
(2)若二面角E-BD-C为30°,求四棱锥P-ABCD的体积.
【答案】(1)见解析(2)![]() a3
a3
【解析】试题分析:(1) 设法证明平面![]() 内的一条直线
内的一条直线![]() 垂直于平面
垂直于平面![]() 内的两条相交直线即可;(2)取
内的两条相交直线即可;(2)取![]() 中点
中点![]() ,连结
,连结![]() ,由已知条件推导出
,由已知条件推导出![]() 为二面角
为二面角![]() 的平面角,由此能求出四棱锥
的平面角,由此能求出四棱锥![]() 的体积
的体积
试题解析:(1)证明 连接OE,如图所示.
∵PO⊥面ABCD,∴PO⊥BD.在正方形ABCD中,BD⊥AC,
又∵PO∩AC=0,∴BD⊥面PAC.
又∵BD面BDE,∴面PAC⊥面BDE.
(2)
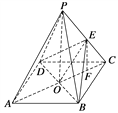 解 取OC中点F,连接EF.
解 取OC中点F,连接EF.
∵E为PC中点,
∴EF为△POC的中位线,∴EF∥PO.
又∵PO⊥面ABCD,
∴EF⊥面ABCD
∵OF⊥BD,∴OE⊥BD.
∴∠EOF为二面角E-BD-C的平面角,
∴∠EOF=30°.
在Rt△OEF中,OF=![]() OC=
OC=![]() AC=
AC=![]() a,∴EF=OF·tan 30°=
a,∴EF=OF·tan 30°=![]() a,∴OP=2EF=
a,∴OP=2EF=![]() a.
a.
∴VP-ABCD=![]() ×a2×
×a2×![]() a=
a=![]() a3.
a3.

练习册系列答案
相关题目