题目内容
【题目】某市为了制定合理的节电方案,供电局对居民用电情况进行了调查,通过抽样,获得了某年200户居民每户的月均用电量(单位:度),将数据按照![]() ,
,![]() 分成9组,制成了如图所示的频率直方图.
分成9组,制成了如图所示的频率直方图.
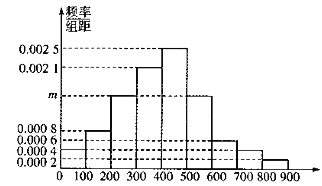
(1)求直方图中![]() 的值并估计居民月均用电量的中位数;
的值并估计居民月均用电量的中位数;
(2)从样本里月均用电量不低于700度的用户中随机抽取4户,用![]() 表示月均用电量不低于800度的用户数,求随机变量
表示月均用电量不低于800度的用户数,求随机变量![]() 的分布列及数学期望.
的分布列及数学期望.
【答案】(Ⅰ)![]() ,中位数为408度.(Ⅱ)
,中位数为408度.(Ⅱ)![]() ,分布列见解析.
,分布列见解析.
【解析】试题分析: (Ⅰ)根据频率分布直方图中小长方形面积等于对应区间概率,而所有概率和为1,列出方程,解出![]() 的值;因为中位数对应概率为
的值;因为中位数对应概率为![]() ,所以先估计中位数所在区间,再根据概率为
,所以先估计中位数所在区间,再根据概率为![]() ,列方程,解出中位数,(Ⅱ)先根据频数等于总数与概率的乘积得200户居民月均用电量在
,列方程,解出中位数,(Ⅱ)先根据频数等于总数与概率的乘积得200户居民月均用电量在![]() 度的户数是8,月均用电量在
度的户数是8,月均用电量在![]() 度的户数是4.再确定随机变量的取法,利用组合数分别计算对应的概率,列表可得分布列,最后根据数学期望公式求期望.
度的户数是4.再确定随机变量的取法,利用组合数分别计算对应的概率,列表可得分布列,最后根据数学期望公式求期望.
试题解析:解:(Ⅰ)![]() ,
,
∴![]() .
.
设中位数是![]() 度,前5组的频率之和为
度,前5组的频率之和为![]() ,
,
而前4组的频率之和为![]() ,
,
所以![]() ,
,![]() ,
,
故![]() ,即居民月均用电量的中位数为408度.
,即居民月均用电量的中位数为408度.
(Ⅱ)200户居民月均用电量在![]() 度的户数是8,月均用电量在
度的户数是8,月均用电量在![]() 度的户数是4.
度的户数是4.
故随机变量![]() 的取值为0,1,2,3,4,且
的取值为0,1,2,3,4,且![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,
所以随机变量![]() 的分布列为:
的分布列为:
| 0 | 1 | 2 | 3 | 4 |
|
|
|
|
|
|
故![]() .
.

 点睛新教材全能解读系列答案
点睛新教材全能解读系列答案 小学教材完全解读系列答案
小学教材完全解读系列答案【题目】某工厂36名工人的年龄数据如下表.
工人编号 年龄 | 工人编号 年龄 | 工人编号 年龄 | 工人编号 年龄 |
1 40 | 10 36 | 19 27 | 28 34 |
2 44 | 11 31 | 20 43 | 29 39 |
3 40 | 12 38 | 21 41 | 30 43 |
4 41 | 13 39 | 22 37 | 31 38 |
5 33 | 14 43 | 23 34 | 32 42 |
6 40 | 15 45 | 24 42 | 33 53 |
7 45 | 16 39 | 25 37 | 34 37 |
8 42 | 17 38 | 26 44 | 35 49 |
9 43 | 18 36 | 27 42 | 36 39 |
(1)用系统抽样法从36名工人中抽取容量为9的样本,且在第一分段里用随机抽样法抽到的年龄数据为44,列出样本的年龄数据;
(2)计算(1)中样本的均值x和方差s2;
(3)36名工人中年龄在![]() 与
与![]() 之间有多少人?所占的百分比是多少(精确到0.01%)?
之间有多少人?所占的百分比是多少(精确到0.01%)?
【题目】某市化工厂三个车间共有工人1 000名,各车间男、女工人数如下表:
第一车间 | 第二车间 | 第三车间 | |
女工 | 173 | 100 | y |
男工 | 177 | x | z |
已知在全厂工人中随机抽取1名,抽到第二车间男工的可能性是0. 15.
(1)求x的值;
(2)现用分层抽样的方法在全厂抽取50名工人,问应在第三车间抽取多少名?