题目内容
【题目】已知椭圆:![]() 的右焦点为
的右焦点为![]() 点的坐标为
点的坐标为![]() ,
,![]() 为坐标原点,
为坐标原点,![]() 是等腰直角三角形.
是等腰直角三角形.
(1)求椭圆![]() 的方程;
的方程;
(2)经过点![]() 作直线
作直线![]() 交椭圆
交椭圆![]() 于
于![]() 两点,求
两点,求![]() 面积的最大值;
面积的最大值;
(3)是否存在直线![]() 交椭圆于
交椭圆于![]() 两点,使点
两点,使点![]() 为
为![]() 的垂心(垂心:三角形三边高线的交点)?若存在,求出直线
的垂心(垂心:三角形三边高线的交点)?若存在,求出直线![]() 的方程;若不存在,请说明理由.
的方程;若不存在,请说明理由.
【答案】(1)![]() ;(2)
;(2)![]() ;(3)
;(3)![]() .
.
【解析】
(1)由![]() 是等腰直角三角形,可得
是等腰直角三角形,可得![]() ,从而可得椭圆方程;
,从而可得椭圆方程;
(2)设过点![]() 的直线
的直线![]() 的方程为
的方程为![]() ,
,![]() 的横坐标分别为
的横坐标分别为![]() ,求出
,求出![]() 的最大值,即可求得
的最大值,即可求得![]() 面积
面积![]() 的最大值;
的最大值;
(3)假设存在直线![]() 交椭圆于
交椭圆于![]() 两点,且使点
两点,且使点![]() 为
为![]() 的垂心,设直线
的垂心,设直线![]() 的方程为
的方程为![]() ,代入椭圆方程,利用韦达定理结合
,代入椭圆方程,利用韦达定理结合![]() ,即可求得结论.
,即可求得结论.
解:(1)由![]() 是等腰直角三角形,可得
是等腰直角三角形,可得![]() ,
,
故椭圆方程为![]() ;
;
(2)设过点![]() 的直线
的直线![]() 的方程为
的方程为![]() ,
,![]() 的横坐标分别为
的横坐标分别为![]() ,
,
将线![]() 的方程为
的方程为![]() 代入椭圆方程,
代入椭圆方程,
消元可得![]() ,
,
∴![]() ,
,
![]() ,
,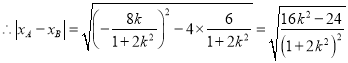 ,
,
令![]() ,则
,则![]()
令![]() ,则
,则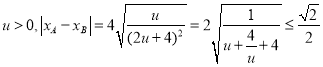 (当且仅当
(当且仅当![]() 时取等号)
时取等号)
又![]() 面积
面积![]() ,
,
∴△AOB面积的最大值为![]() ;
;
(3)假设存在直线![]() 交椭圆于
交椭圆于![]() 两点,且使点
两点,且使点![]() 为
为![]() 的垂心,
的垂心,
设![]() ,
,
因为![]() ,所以
,所以![]() .
.
于是设直线![]() 的方程为
的方程为![]() ,代入椭圆方程,
,代入椭圆方程,
消元可得![]() .
.
由![]() ,得
,得![]() ,且
,且![]() ,
,
由题意应有![]() ,所以
,所以![]() ,
,
所以![]() .
.
整理得![]() .
.
解得![]() 或
或![]() .
.
经检验,当![]() 时,
时,![]() 不存在,故舍去.
不存在,故舍去.
∴当![]() 时,所求直线
时,所求直线![]() 存在,且直线l的方程
存在,且直线l的方程![]()

练习册系列答案
相关题目
【题目】从某大学中随机选取7名女大学生,其身高x(单位:cm)和体重y(单位:kg)数据如下表:
编号 | 1 | 2 | 3 | 4 | 5 | 6 | 7 |
身高x | 163 | 164 | 165 | 166 | 167 | 168 | 169 |
体重y | 52 | 52 | 53 | 55 | 54 | 56 | 56 |
(1)求y关于x的回归方程;
(2)利用(1)中的回归方程,分析这7名女大学生的身高和体重的变化,并预报一名身高为172cm的女大学生的体重.