题目内容
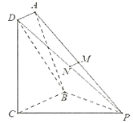
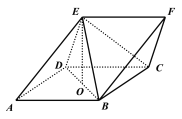
【题目】如图,在三棱柱![]() 中,侧面
中,侧面![]() 是为菱形,
是为菱形,![]() 在平面
在平面![]() 内的射影
内的射影![]() 恰为线段
恰为线段![]() 的中点.
的中点.
(1)求证:![]() ;
;
(2)若![]() ,
,![]() ,求二面角
,求二面角![]() 的平面角的余弦值.
的平面角的余弦值.
【答案】(1)证明见解析(2)![]()
【解析】
(1)连接![]() ,由线面垂直的判定方法可证得
,由线面垂直的判定方法可证得![]() 面
面![]() ,从而得到
,从而得到![]() ,根据平行关系可证得结论;
,根据平行关系可证得结论;
(2)以![]() 为坐标原点建立空间直角坐标系,利用二面角的空间向量求法可求得结果.
为坐标原点建立空间直角坐标系,利用二面角的空间向量求法可求得结果.
(1)证明:如图,连接![]() ,易知
,易知![]() .
.
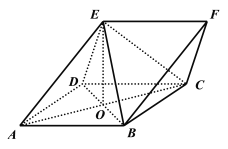
∵侧面![]() 是菱形,∴
是菱形,∴![]() .
.
由射影定义可知:![]() 面
面![]() ,又
,又![]() 面
面![]() ,∴
,∴![]() ,
,
而![]() ,且
,且![]() ,
,![]() 面
面![]() ,∴
,∴![]() 面
面![]() ,
,
![]() 平面
平面![]() ,∴
,∴![]() .
.
∵![]() ,∴
,∴![]() .
.
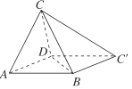
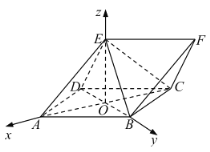
(2)由(1)知:![]() ,
,![]() ,
,![]() ,,于是以
,,于是以![]() 为坐标原点,
为坐标原点,![]() ,
,![]() ,
,![]() 所在直线分别为
所在直线分别为![]() ,
,![]() ,
,![]() 轴建立空间直角坐标系,如图所示:
轴建立空间直角坐标系,如图所示:
不妨设![]() .
.
∵在菱形![]() 中,
中,![]() ,∴
,∴![]() ,
,![]() .
.
在![]() 中,
中,![]() .
.
于是![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,
∴![]() ,
,![]() ,
,![]() .
.
又由![]() ,可解得:
,可解得:![]() ,
,![]() .
.
设平面![]() 的法向量为
的法向量为![]() ,
,
则由![]() ,
,![]() 得
得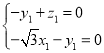 ,
,
令![]() ,则
,则![]() ,
,![]() ,即
,即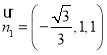 .
.
同理可得平面![]() 的法向量
的法向量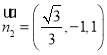 .
.
∴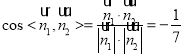 ,
,
![]() 二面角
二面角![]() 的平面角为锐角,
的平面角为锐角,![]() 所求的余弦值为
所求的余弦值为![]() .
.

练习册系列答案
相关题目
【题目】车工刘师傅利用数控车床为某公司加工一种高科技易损零件,对之前加工的100个零件的加工时间进行统计,结果如下:
加工1个零件用时 | 20 | 25 | 30 | 35 |
频数(个) | 15 | 30 | 40 | 15 |
以加工这100个零件用时的频率代替概率.
(1)求![]() 的分布列与数学期望
的分布列与数学期望![]() ;
;
(2)刘师傅准备给几个徒弟做一个加工该零件的讲座,用时40分钟,另外他打算在讲座前、讲座后各加工1个该零件作示范.求刘师傅讲座及加工2个零件作示范的总时间不超过100分钟的概率.