题目内容
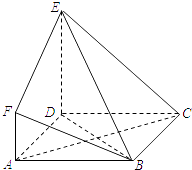
【题目】如图,在直四棱柱![]() 中,底面
中,底面![]() 是边长为2的正方形,
是边长为2的正方形, ![]() 分别为线段
分别为线段![]() ,
, ![]() 的中点.
的中点.

(1)求证: ![]() ||平面
||平面![]() ;
;
(2)四棱柱![]() 的外接球的表面积为
的外接球的表面积为![]() ,求异面直线
,求异面直线![]() 与
与![]() 所成的角的大小.
所成的角的大小.
【答案】(1)见解析;(2)![]()
【解析】试题分析:(1)连接BD1,由中位线定理证明EF∥D1B,由线面平行的判定定理证明EF∥平面ABC1D1;
(2)由(1)和异面直线所成角的定义,得异面直线EF与BC所成的角是∠D1BC,由题意和球的表面积公式求出外接球的半径,由勾股定理求出侧棱AA1的长,由直四棱柱的结构特征和线面垂直的定义,判断出BC⊥CD1,在RT△CC1D1中求出tan∠D1BC,求出∠D1BC可得答案.
试题解析:
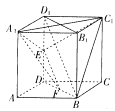
(1)连接![]() ,在
,在![]() 中,
中, ![]() 分别为线段
分别为线段![]() 的中点,∴
的中点,∴![]() 为中位线,
为中位线,
∴![]() ,而
,而![]() 面
面![]() ,
, ![]() 面
面![]() ,∴
,∴![]() 平面
平面![]() .
.
(2)由(1)知![]() ,故
,故![]() 即为异面直线
即为异面直线![]() 与
与![]() 所成的角.
所成的角.
∵四棱柱![]() 的外接球的表面积为
的外接球的表面积为![]() ,
,
∴四棱柱![]() 的外接球的半径
的外接球的半径![]() ,
,
设![]() ,则
,则![]() ,解得
,解得![]() ,
,
在直四棱柱![]() 中,∵
中,∵![]() 平面
平面![]() ,
, ![]() 平面
平面![]() ,
,
∴![]() ,在
,在![]() 中,
中, ![]() ,
,
∴![]() ,
,
∴异面直线![]() 与
与![]() 所成的角为
所成的角为![]() .
.

练习册系列答案
相关题目