题目内容
【题目】如图,ABCD是边长为3的正方形,DE⊥平面ABCD,AF∥DE,DE=3AF,BE与平面ABCD所成角为60°. 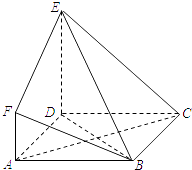
(1)求证:AC⊥平面BDE;
(2)设点M是线段BD上一个动点,试确定点M的位置,使得AM∥平面BEF,并证明你的结论.
【答案】
(1)证明:因为DE⊥平面ABCD,
所以DE⊥AC.
因为ABCD是正方形,
所以AC⊥BD,因为DE∩BD=D
从而AC⊥平面BDE.
(2)解:当M是BD的一个三等分点,即3BM=BD时,AM∥平面BEF.
取BE上的三等分点N,使3BN=BE,连接MN,NF,则DE∥MN,且DE=3MN,
因为AF∥DE,且DE=3AF,所以AF∥MN,且AF=MN,
故四边形AMNF是平行四边形.
所以AM∥FN,
因为AM平面BEF,FN平面BEF,
所以AM∥平面BEF.
【解析】(1)根据DE⊥平面ABCD,由线面垂直的判定定理可知DE⊥AC,由ABCD是正方形可知AC⊥BD,而DE∩BD=D,满足线面垂直的判定所需条件,从而证得结论;(2)当M是BD的一个三等分点,即3BM=BD时,AM∥平面BEF.取BE上的三等分点N,使3BN=BE,连接MN,NF,则DE∥MN,且DE=3MN,而AF∥DE,且DE=3AF,则四边形AMNF是平行四边形,从而AM∥FN,AM平面BEF,FN平面BEF,满足线面平行的判定定理,从而证得结论.
【考点精析】本题主要考查了直线与平面平行的判定和直线与平面垂直的判定的相关知识点,需要掌握平面外一条直线与此平面内的一条直线平行,则该直线与此平面平行;简记为:线线平行,则线面平行;一条直线与一个平面内的两条相交直线都垂直,则该直线与此平面垂直;注意点:a)定理中的“两条相交直线”这一条件不可忽视;b)定理体现了“直线与平面垂直”与“直线与直线垂直”互相转化的数学思想才能正确解答此题.