题目内容
【题目】已知椭圆C： 
=1（a＞b＞0）的右焦点为F，上顶点为A，短轴长为2，O为原点，直线AF与椭圆C的另一个交点为B，且△AOF的面积是△BOF的面积的3倍．
（1）求椭圆C的方程；
（2）如图，直线l：y=kx+m与椭圆C相交于P，Q两点，若在椭圆C上存在点R，使OPRQ为平行四边形，求m的取值范围．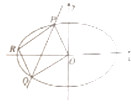 
【答案】
（1）解：短轴长为2，可得b=1，
即有A（0，1），设F（c，0），B（x0，y0），
△AOF的面积是△BOF的面积的3倍，
即为 
c1=3 c|y0|，
可得y0=﹣ 
，由直线AF：y=﹣ 
+1经过B，
可得x0= 
c，即B（ c，﹣ ），代入椭圆方程可得，
+ 
=1，即为a2=2c2，即有a2=2b2=2，
则椭圆方程为 
+y2=1
（2）解：设P（x1，y1），Q（x2，y2），
由OPRQ为平行四边形，可得x1+x2=xR，y1+y2=yR，
R在椭圆C上，可得 
+（y1+y2）2=1，
即为 +（k（x1+x2）+2m）2=1，
化为（1+2k2）（（x1+x2）2+8km（x1+x2）+8m2=2，①
由 
可得（1+2k2）x2+4kmx+2m2﹣2=0，
由△=16k2m2﹣4（1+2k2）（2m2﹣2）＞0，即为1+2k2＞m2，②
x1+x2=﹣ 
，代入①可得 
﹣ 
+8m2=2，
化为1+2k2=4m2，代入②可得m≠0，
又4m2=1+2k2≥1，解得m≥ 或m≤﹣ ．
则m的取值范围是（﹣∞，﹣ ]∪[ ，+∞）
【解析】（1）由题意可得b=1，A（0，1），设F（c，0），B（x0 ， yspan>0），运用三角形的面积公式可得y0=﹣ ，再由直线AF的方程经过B，可得B的坐标，代入椭圆方程，解得a，b，进而得到椭圆方程；（2）设P（x1 ， y1），Q（x2 ， y2），由OPRQ为平行四边形，可得x1+x2=xR ， y1+y2=yR ， R在椭圆C上，代入椭圆方程，再由直线l与椭圆方程联立，运用韦达定理和判别式大于0，化简整理，解不等式即可得到所求m的范围．
