题目内容
若函数 恰有三个单调区间,则实数
恰有三个单调区间,则实数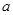 的取值范围为 ( )
的取值范围为 ( )
 恰有三个单调区间,则实数
恰有三个单调区间,则实数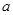 的取值范围为 ( )
的取值范围为 ( ) A.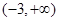 | B.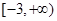 | C. | D.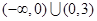 |
C
试题分析:由题意知,f′(x)=3ax2+6x-1,
∵f(x)恰有三个单调区间,
∴f′(x)=3ax2+6x-1=0有两个不同的实数根,
∴△=36-4×3a×(-1)>0,且a≠0,即a>-3且a≠0,即(-3,0)∪(0,+∞),故选C.
点评:简单题,关键是认识到f′(x)=3ax2+6x-1=0有两个不同的实数根。易错点是忽视对二次项系数的讨论。

练习册系列答案
 课堂全解字词句段篇章系列答案
课堂全解字词句段篇章系列答案 步步高口算题卡系列答案
步步高口算题卡系列答案
相关题目
 .
. ,
,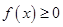 对一切
对一切 恒成立,求
恒成立,求 的最大值;
的最大值; ,且
,且 、
、 是曲线
是曲线 上任意两点,若对任意
上任意两点,若对任意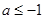 ,直线
,直线 的斜率恒大于常数
的斜率恒大于常数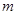 ,求
,求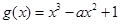 在区间
在区间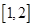 上是单调递减函数,则实数
上是单调递减函数,则实数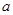 的取值范围是 .
的取值范围是 .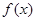 ,
,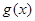 都是定义在R上的函数,
都是定义在R上的函数,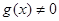 ,
,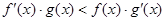 ,
,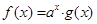
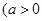 ,且
,且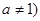 ,
,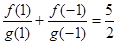 ,在有穷数列
,在有穷数列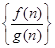
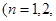
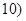 中,任意取正整数
中,任意取正整数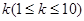 ,则前
,则前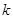 项和大于
项和大于 的概率是
的概率是 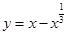 的图象大致为( )
的图象大致为( )
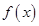 在R 上可导,且满足
在R 上可导,且满足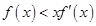 ,则( )
,则( )



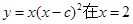 处有极大值,则常数c= ;
处有极大值,则常数c= ;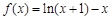 .
.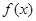 的单调递减区间;
的单调递减区间;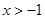 ,证明:
,证明: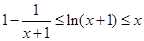 .
.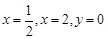 ,及曲线
,及曲线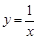 所围图形的面积为( )
所围图形的面积为( )


