Question

【题目】已知椭圆离心率为，点与椭圆的左、右顶点可以构成等腰直角三角形．点C是椭圆的下顶点，经过椭圆中心O的一条直线与椭圆交于A，B两个点（不与点C重合），直线CA，CB分别与x轴交于点D，E．

（1）求椭圆的标准方程．

（2）判断的大小是否为定值，并证明你的结论．

Answer 1

【答案】（1）（2）是定值．证明见解析

【解析】

（1）根据椭圆离心率，以及点与椭圆的左、右顶点可以构成等腰直角三角形，求得的值，由此求得椭圆的标准方程.

（2）设出两点的坐标，求得直线的方程，由此求得点的坐标，同理求得点的坐标，通过计算，证得，从而证得为定值.

（1）依题意可知.由于点与椭圆的左、右顶点可以构成等腰直角三角形，所以，故，所以.

所以椭圆方程为．

（2）是定值．

设，

则直线CA的方程为．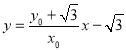

将代入，解得，即．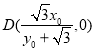

同理，解得．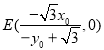

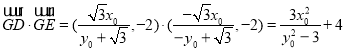
将代入上式，得．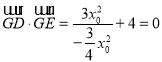

所以，即证．