Question

【题目】函数的部分图象如图所示，其中，，.

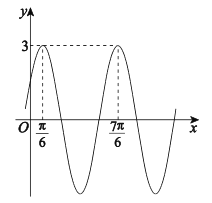
（Ⅰ）求的解析式；

（Ⅱ）求在区间上的最大值和最小值；

（Ⅲ）写出的单调递增区间.

Answer 1

【答案】（Ⅰ）；（Ⅱ）最大值为，最小值为；（Ⅲ）单调递增区间为.

【解析】

（Ⅰ）由函数的最大值可求得的值，从图象可得出函数的最小正周期，可求得的值，再将点的坐标代入函数的解析式，结合可求得的值，进而可求得函数的解析式；

（Ⅱ）由可求得的取值范围，结合正弦函数的基本性质可求得函数在区间上的最大值和最小值；

（Ⅲ）解不等式，可得出函数的单调递增区间.

（Ⅰ）由图象可得，

且函数的最小正周期为，，

，得，

，，，可得.

因此，；

（Ⅱ），，

所以，当时，函数取得最小值，即；

当时，函数取得最大值，即.

因此，函数在区间上的最大值为，最小值为；

（Ⅲ）解不等式，得.

所以，函数的单调递增区间为.