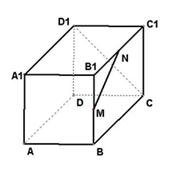
题目内容
已知某几何体的三视图如下图所示,其中左视图是边长为2的正三角形,主视图是矩形且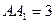 ,俯视图中
,俯视图中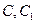 分别是所在边的中点,设
分别是所在边的中点,设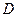 为
为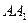 的中点.
的中点.
(1)求其体积;(2)求证: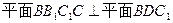 ;
;
(3)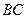 边上是否存在点
边上是否存在点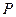 ,使
,使 ?若不存在,说明理由;若存在,请证明你的结论.
?若不存在,说明理由;若存在,请证明你的结论.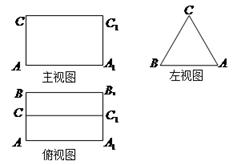
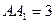 ,俯视图中
,俯视图中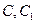 分别是所在边的中点,设
分别是所在边的中点,设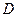 为
为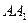 的中点.
的中点.(1)求其体积;(2)求证:
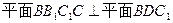 ;
;(3)
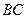 边上是否存在点
边上是否存在点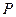 ,使
,使 ?若不存在,说明理由;若存在,请证明你的结论.
?若不存在,说明理由;若存在,请证明你的结论.
(1)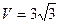 (2)见解析(3)当
(2)见解析(3)当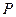 与
与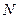 重合即
重合即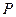 为边
为边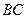 的中点时,使
的中点时,使
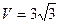 (2)见解析(3)当
(2)见解析(3)当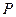 与
与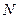 重合即
重合即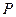 为边
为边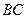 的中点时,使
的中点时,使
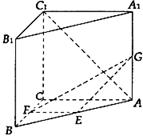
(1)该几何体的直观图为平放正三棱柱且体积为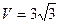 ...........4分
...........4分
(2)取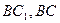 的中点分别为
的中点分别为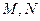 ,连接
,连接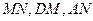 ,由正三棱柱的性质得
,由正三棱柱的性质得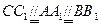 ,又
,又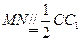 ,
,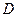 为
为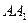 的中点, ∴
的中点, ∴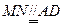
∴四边形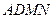 为平行四边形 ∴
为平行四边形 ∴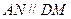
由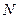 正三角形的边
正三角形的边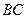 的中点 ∴
的中点 ∴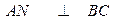
又由正三棱柱的性质得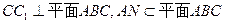 , ∴
, ∴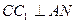 且
且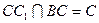 ∴
∴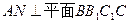 ∴
∴
又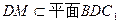 ∴
∴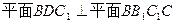 ……………………10分
……………………10分
(3)由(2)知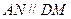 ,且
,且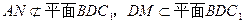 ∴
∴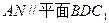
故当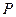 与
与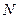 重合即
重合即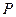 为边
为边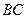 的中点时,使
的中点时,使 ………….16分
………….16分
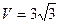 ...........4分
...........4分(2)取
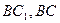 的中点分别为
的中点分别为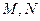 ,连接
,连接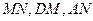 ,由正三棱柱的性质得
,由正三棱柱的性质得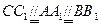 ,又
,又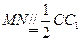 ,
,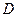 为
为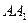 的中点, ∴
的中点, ∴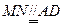
∴四边形
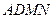 为平行四边形 ∴
为平行四边形 ∴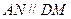
由
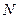 正三角形的边
正三角形的边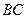 的中点 ∴
的中点 ∴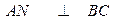
又由正三棱柱的性质得
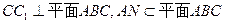 , ∴
, ∴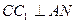 且
且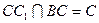 ∴
∴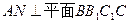 ∴
∴
又
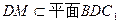 ∴
∴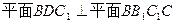 ……………………10分
……………………10分(3)由(2)知
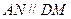 ,且
,且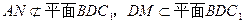 ∴
∴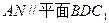
故当
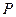 与
与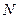 重合即
重合即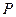 为边
为边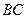 的中点时,使
的中点时,使 ………….16分
………….16分
练习册系列答案
 优翼小帮手同步口算系列答案
优翼小帮手同步口算系列答案
相关题目
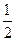 BD
BD
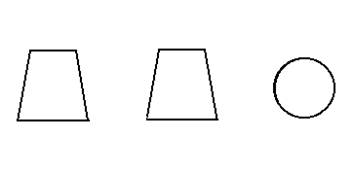
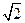 ,AC=3,BC=
,AC=3,BC=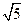 ,D是A1C的中点E是侧棱BB1上的一动点。
,D是A1C的中点E是侧棱BB1上的一动点。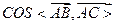 的值
的值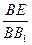 的值,不存在则说明理由。
的值,不存在则说明理由。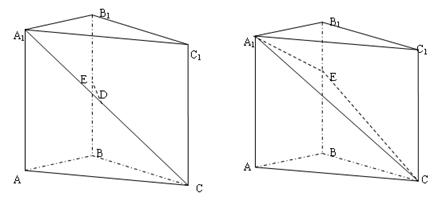
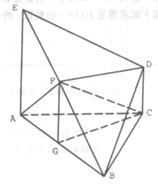
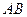 、
、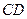 的长度分别等于
的长度分别等于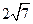 、
、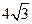 ,
,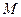 、
、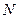 分别为
分别为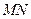 的最大值为5 ④
的最大值为5 ④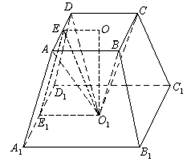
 的棱
的棱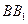 和
和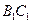 的中点,求:
的中点,求: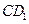 所成的角;
所成的角;