题目内容
(本小题满分13分)
已知数列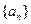 满足:
满足: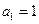 ,
,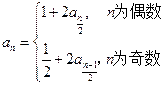
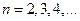
(I)求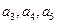 得值;
得值;
(II)设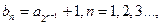 求证:数列
求证:数列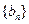 是等比数列,并求出其通项公式;
是等比数列,并求出其通项公式;
(III)对任意的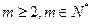 ,在数列
,在数列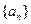 中是否存在连续的
中是否存在连续的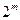 项构成等差数列?若存在,写出这
项构成等差数列?若存在,写出这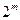 项,并证
项,并证 明这
明这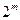 项构成等差数列;若不存在,说明理由.
项构成等差数列;若不存在,说明理由.
已知数列
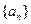 满足:
满足: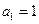 ,
,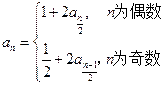
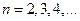
(I)求
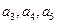 得值;
得值;(II)设
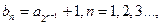 求证:数列
求证:数列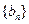 是等比数列,并求出其通项公式;
是等比数列,并求出其通项公式;(III)对任意的
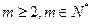 ,在数列
,在数列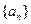 中是否存在连续的
中是否存在连续的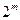 项构成等差数列?若存在,写出这
项构成等差数列?若存在,写出这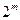 项,并证
项,并证 明这
明这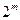 项构成等差数列;若不存在,说明理由.
项构成等差数列;若不存在,说明理由.解:(I)因为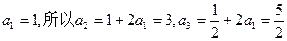 ,
,
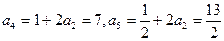 ………………3分
………………3分
(II)由题意,对于任意的正整数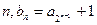 ,
,
所以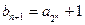 ………………4分
………………4分
又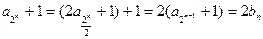
所以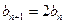 ………………6分
………………6分
又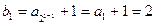 ………………7分
………………7分
所以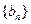 是首项为2,公比为2的等比数列,所以
是首项为2,公比为2的等比数列,所以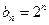 ………………8分
………………8分
(III)存在,事实上,对任意的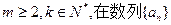 中,
中,
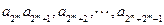 这连续的
这连续的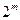 项就构成一个等差数列………………10分
项就构成一个等差数列………………10分
我们先来证明:
“对任意的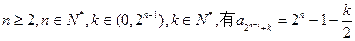 ”
”
由(II)得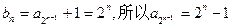
当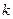 为奇数时,
为奇数时,
当k为偶数时,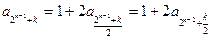
记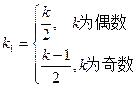
因此要证
其中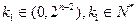
(这是因为若 时,则k一定是奇数)
时,则k一定是奇数)
有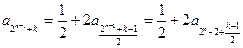
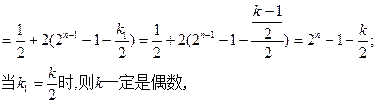
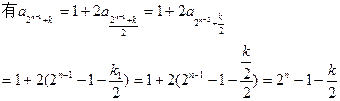
如此递推,要证
其中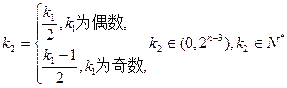
如此递推下去,我们只需证明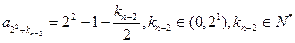
即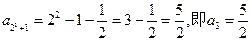 ,由(I)可得,
,由(I)可得,
所以对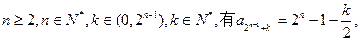
对任意的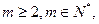
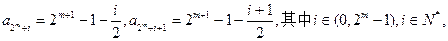
所以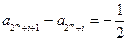
又
所以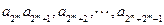 这连续的
这连续的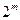 项,
项,
是首项为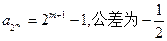 的等差数列。 ………………13分
的等差数列。 ………………13分
 说明:当
说明:当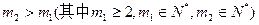 时,
时,
因为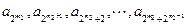 构成一个项数为
构成一个项数为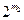 的等差数列,所以从这个数列中任取连续的
的等差数列,所以从这个数列中任取连续的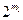 项,也是一个项数为
项,也是一个项数为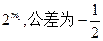 的等差数列。
的等差数列。
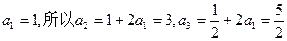 ,
,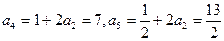 ………………3分
………………3分(II)由题意,对于任意的正整数
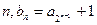 ,
,所以
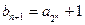 ………………4分
………………4分又
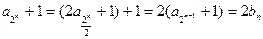
所以
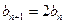 ………………6分
………………6分又
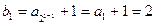 ………………7分
………………7分所以
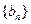 是首项为2,公比为2的等比数列,所以
是首项为2,公比为2的等比数列,所以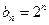 ………………8分
………………8分(III)存在,事实上,对任意的
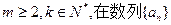 中,
中,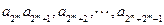 这连续的
这连续的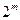 项就构成一个等差数列………………10分
项就构成一个等差数列………………10分我们先来证明:
“对任意的
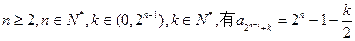 ”
”由(II)得
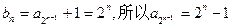
当
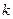 为奇数时,
为奇数时,
当k为偶数时,
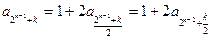
记
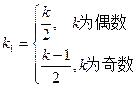
因此要证

其中
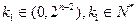
(这是因为若
 时,则k一定是奇数)
时,则k一定是奇数)有
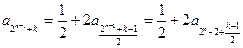
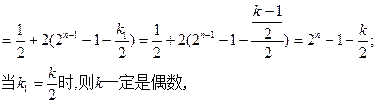
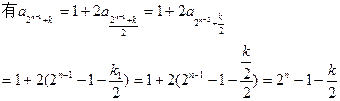
如此递推,要证

其中
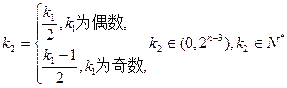
如此递推下去,我们只需证明
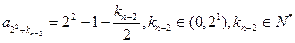
即
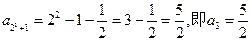 ,由(I)可得,
,由(I)可得,所以对
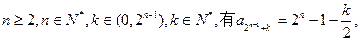
对任意的
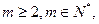
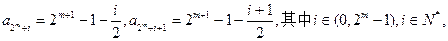
所以
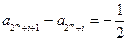
又

所以
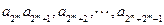 这连续的
这连续的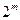 项,
项,是首项为
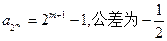 的等差数列。 ………………13分
的等差数列。 ………………13分 说明:当
说明:当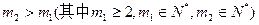 时,
时,因为
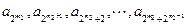 构成一个项数为
构成一个项数为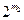 的等差数列,所以从这个数列中任取连续的
的等差数列,所以从这个数列中任取连续的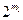 项,也是一个项数为
项,也是一个项数为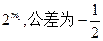 的等差数列。
的等差数列。略

练习册系列答案
相关题目
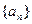 的前n项和为
的前n项和为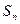 ,且满足
,且满足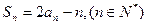
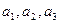 的值;
的值;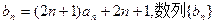 的前n项和为
的前n项和为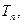 求满足不等式
求满足不等式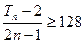 的最小n值.
的最小n值.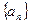 满足
满足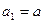 ,
,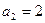 ,
,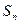 是数列的前
是数列的前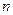 项和,且
项和,且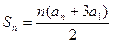 (
(
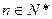 ).
).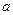 的值;
的值; 列
列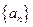 的通项公式;
的通项公式; (3)对于数列
(3)对于数列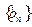 ,若存在常数M,使
,若存在常数M,使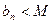 (
(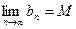 ,则M叫做数列
,则M叫做数列 (
(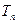 为数列
为数列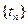 的前
的前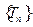 的上渐近值.
的上渐近值.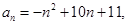 则数列
则数列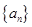 从首项到第几项的和最大( )
从首项到第几项的和最大( )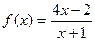
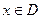 ,构造一个数列发生器,其工作原理如下:
,构造一个数列发生器,其工作原理如下: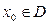 ,经数列发生器输出
,经数列发生器输出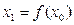 ,若
,若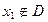 ,则数列发生器结束工作,
,则数列发生器结束工作,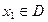 ,则将
,则将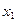 反馈回输入端,再输出
反馈回输入端,再输出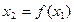 并依此规律继续下去,若输入
并依此规律继续下去,若输入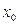 时,产生的无穷数列
时,产生的无穷数列 满足,对任意正整数
满足,对任意正整数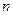 均有
均有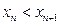 ,求
,求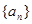 为等差数列,
为等差数列,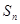 是其前n项和,且
是其前n项和,且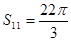 ,则
,则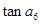 的值为 ( )
的值为 ( )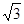
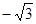
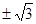
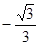
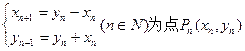 到点
到点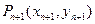 的一个变换为“
的一个变换为“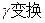 ”,已知
”,已知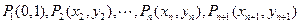 是经过“
是经过“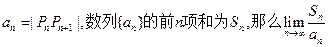 的值为 ( )
的值为 ( )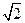
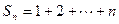
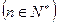 ,
,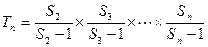
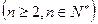 ,则下列各数中与
,则下列各数中与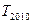 最接近的数是( )
最接近的数是( )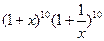 展开式中的常数项为
展开式中的常数项为