题目内容
(本小题满分12分)
已知数列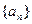 的前n项和为
的前n项和为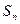 ,且满足
,且满足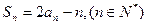
(1)求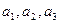 的值;
的值;
(2)求数列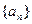 的通项公式;
的通项公式;
(3)若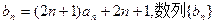 的前n项和为
的前n项和为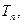 求满足不等式
求满足不等式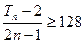 的最小n值.
的最小n值.
已知数列
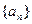 的前n项和为
的前n项和为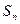 ,且满足
,且满足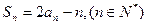
(1)求
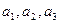 的值;
的值;(2)求数列
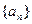 的通项公式;
的通项公式;(3)若
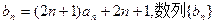 的前n项和为
的前n项和为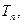 求满足不等式
求满足不等式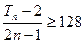 的最小n值.
的最小n值.(1)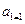 ,
,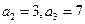 (2)
(2)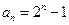 (3)6
(3)6
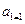 ,
,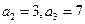 (2)
(2)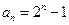 (3)6
(3)6(1 )因为
)因为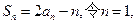
解得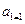 …………1分
…………1分
再分别令n=2,n=3,解得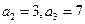 …………3分
…………3分
 (2)因为
(2)因为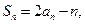
所以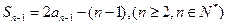
两式相减得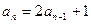
所以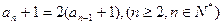
又因为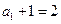 ,所以
,所以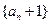 是首项为2,公比为2的等比数列
是首项为2,公比为2的等比数列
所以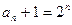 ,所以
,所以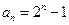 …………7分
…………7分
(3)因为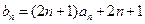 ,
,
所以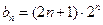
所以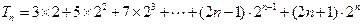 ①
①
 ②
②
①—②得: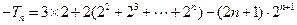

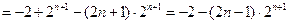
所以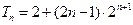 …………10分
…………10分
若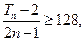
则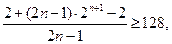
即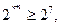 所以
所以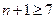 ,解得
,解得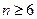 ,
,
所以满足不等式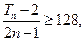 的最小n值6,…………12分
的最小n值6,…………12分
 )因为
)因为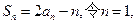
解得
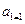 …………1分
…………1分再分别令n=2,n=3,解得
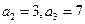 …………3分
…………3分 (2)因为
(2)因为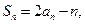
所以
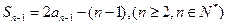
两式相减得
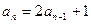
所以
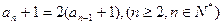
又因为
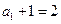 ,所以
,所以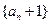 是首项为2,公比为2的等比数列
是首项为2,公比为2的等比数列所以
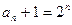 ,所以
,所以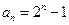 …………7分
…………7分(3)因为
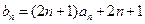 ,
,所以
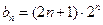
所以
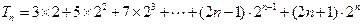 ①
① ②
②①—②得:
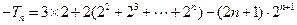

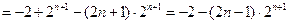
所以
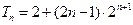 …………10分
…………10分若
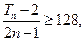
则
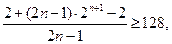
即
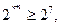 所以
所以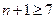 ,解得
,解得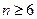 ,
,所以满足不等式
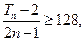 的最小n值6,…………12分
的最小n值6,…………12分
练习册系列答案
相关题目
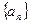 是公差为
是公差为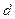
 的等差数列,数列
的等差数列,数列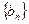 是公比为
是公比为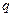 的(q∈R)的等比数列,若函数
的(q∈R)的等比数列,若函数 ,且
,且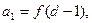
 ,
,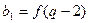 ,
,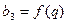 ,
,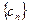 的前n项和为
的前n项和为 ,对一切
,对一切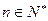 ,都有
,都有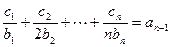 成立,求
成立,求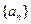 的前n项和为
的前n项和为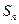 ,数列
,数列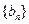 满足:
满足: 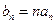 ,且数列
,且数列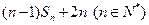 .
.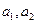 的值;
的值;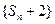 是等比数列;
是等比数列;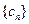 ,若
,若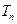 ,求证:
,求证: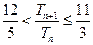 .
.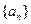 满足:
满足: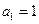 ,
,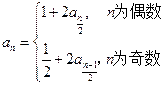
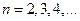
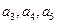 得值;
得值;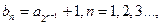 求证:数列
求证:数列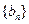 是等比数列,并求出其通项公式;
是等比数列,并求出其通项公式;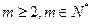 ,在数列
,在数列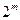 项构成等差数列?若存在,写出这
项构成等差数列?若存在,写出这 明这
明这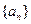 的前
的前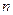 项和为
项和为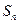 ,且满足
,且满足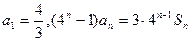
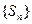 的通项公式;
的通项公式;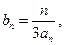 求为数列
求为数列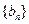 的前
的前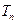 。
。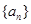 的前
的前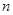 项的和
项的和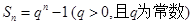 ,某同学得出如下三个结论:①
,某同学得出如下三个结论:①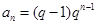 ;②
;②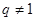 时,
时,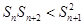 ,
,
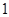
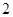
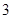
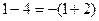 ,
,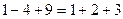 ,
,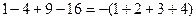 ,…归纳出第
,…归纳出第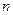 个式子为_______________________.
个式子为_______________________. 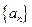 的前
的前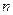 项和为
项和为 ,且
,且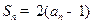 ,则
,则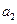 ( )
( ) 
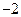
 3a4=7a7,且a1>0,Sn是数列{an}前n项的和,若Sn取得最大值,则n= .
3a4=7a7,且a1>0,Sn是数列{an}前n项的和,若Sn取得最大值,则n= .