Question

【题目】对给定自然数n≥2，求满足下列条件的最大的N：无论怎样将填人一个n×n的方格表，总存在同一行或同一列的两个数，它们的差不小于N。

Answer 1

【答案】

【解析】

首先构造具体的例子证明：

.

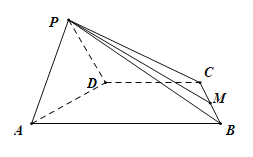
1 当n为偶数时，设n=2k.如图，将方格表等分为A、B、C、D四个k×k的区域，按如下方式填数

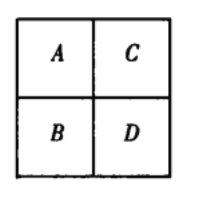
区域A中的填法为

1 2 ... k

k+1 k+2 ... 2k

... ... ... ...

k(k-1)+1 k(k-1)+2 ...

区域B中的填法为将区域A中的每个数均加上，类似地填区域C和D，所加数分别为2、3.

2 当n为奇数时，设n=2k+1.如图，方格表的中间一行和中间一列将其余部分划成了A、B、C、D四个k×k的区域，按如下方式填数.

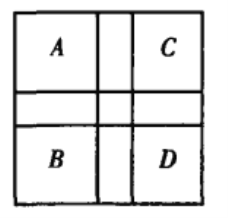
区域A的填法与n为偶数时相同，区域B、C、D的填法分别为将区域A中的数加上

；

中间一行的数从左至右依次为，

；

中间一列的数从上至下依次为

.

容易验证，对以上的填法，方格表中同一行或同一列的任两个数之差均不大于:.

其次，对任意一种填法，设占据了x行y列，即这个数均在这x行y列的交叉处.于是，([x]表示不超过实数x的最大整数).

则

.①

设占据了z行w列.类似有

. ②

由式①、②知.

因此，存在中的一个数(设为u)与

.中的一个数(设为u)在同一行或同一列,且有

(注意到，中必有一个为整数).

可见，N满足要求.

综上，N的最大值为.