题目内容
【题目】已知![]() ,
,![]() ,点
,点![]() 满足
满足![]() ,记点
,记点![]() 的轨迹为
的轨迹为![]() .
.
(1)求轨迹![]() 的方程;
的方程;
(2)若直线![]() 过点
过点![]() 且与轨迹
且与轨迹![]() 交于
交于![]() 、
、![]() 两点.
两点.
(i)无论直线![]() 绕点
绕点![]() 怎样转动,在
怎样转动,在![]() 轴上总存在定点
轴上总存在定点![]() ,使
,使![]() 恒成立,求实数
恒成立,求实数![]() 的值.
的值.
(ii)在(i)的条件下,求![]() 面积的最小值.
面积的最小值.
【答案】(1)![]() (2)(i)
(2)(i)![]() (ii)9
(ii)9
【解析】
(1)利用双曲线的定义及其标准方程即可得出;(2)当直线l的斜率存在时,设直线方程为y=k(x-2),P![]() ,Q
,Q![]() ,与双曲线方程联立消y得
,与双曲线方程联立消y得![]() ,利用根与系数的关系、判别式解出即可得出.(i)利用向量垂直与数量积的关系、根与系数的关系即可得出;(ii)利用点到直线的距离公式、弦长公式、点到直线的距离公式、三角形的面积计算公式即可得出
,利用根与系数的关系、判别式解出即可得出.(i)利用向量垂直与数量积的关系、根与系数的关系即可得出;(ii)利用点到直线的距离公式、弦长公式、点到直线的距离公式、三角形的面积计算公式即可得出
(1)由![]() 知,点P的轨迹E是以F1、F2为焦点的双曲线右支,由
知,点P的轨迹E是以F1、F2为焦点的双曲线右支,由![]() ,故轨迹E的方程为
,故轨迹E的方程为![]()
(2)当直线l的斜率存在时,设直线方程为![]() ,与双曲线方程联立消y得
,与双曲线方程联立消y得![]() ,
,
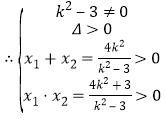 解得k2 >3
解得k2 >3
(i)![]()
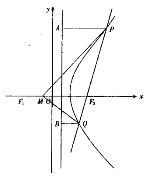
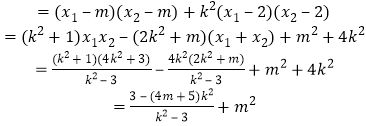
![]() ,
,
故得![]() 对任意的
对任意的![]() 恒成立,
恒成立,
![]() ∴当m =-1时,MP⊥MQ.
∴当m =-1时,MP⊥MQ.
当直线l的斜率不存在时,由![]() 知结论也成立,
知结论也成立,
综上,当m =-1时,MP⊥MQ.
(ii)由(i)知,![]() ,当直线l的斜率存在时,
,当直线l的斜率存在时,
![]() , M点到直线PQ的距离为
, M点到直线PQ的距离为![]() ,则
,则![]()
∴![]()
令![]() ,则
,则![]() ,因为
,因为![]()
所以![]()
当直线l的斜率不存在时,![]()
综上可知![]() ,故
,故![]() 的最小值为9.
的最小值为9.

 超能学典应用题题卡系列答案
超能学典应用题题卡系列答案【题目】已知某中学高三文科班学生共有800人参加了数学与地理的水平测试,学校决定利用随机数表法从中抽取100人进行成绩抽样调查.抽取的100人的数学与地理的水平测试成绩如下表:
人数 | 数学 | |||
优秀 | 良好 | 及格 | ||
地理 | 优秀 | 7 | 20 | 5 |
良好 | 9 | 18 | 6 | |
及格 | a | 4 | b | |
成绩分为优秀、良好、及格三个等级;横向,纵向分别表示地理成绩与数学成绩,例如:表中数学成绩为良好的共有20+18+4=42人.
(1)在该样本中,数学成绩优秀率是30%,求a,b的值;
(2)在地理成绩及格的学生中,已知a≥10,b≥7,求数学成绩优秀的人数比及格的人数少的概率.
【题目】某市预测2000年到2004年人口总数与年份的关系如下表所示
年份200x(年) | 0 | 1 | 2 | 3 | 4 |
人口数y(十)万 | 5 | 7 | 8 | 11 | 19 |
(1)请根据上表提供的数据,计算![]() ,用最小二乘法求出
,用最小二乘法求出![]() 关于
关于![]() 的线性回归方程
的线性回归方程![]()
(2) 据此估计2005年该城市人口总数。
(参考数值:0×5+1×7+2×8+3×11+4×19=132,![]()
参考公式:用最小二乘法求线性回归方程系数公式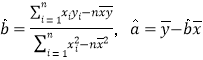 )
)