题目内容
【题目】已知
，函数
（1）讨论函数
的单调性；
（2）若函数
有两个不同的零点
，求实数
的取值范围；
（3）在（2）的条件下，求证： 
【答案】（1）在 
是增函数， 
是减函数；（2）
；（3）证明见解析.
【解析】试题分析：（1）先求导，再分类讨论，分别令 
可得增区间，令
可得得减区间；(2)讨论两种情况，分别利用导数判断函数的单调性，以及结合函数的极值及简图即可求出
的范围；（3）由
，只要证明： 
就可以得出结论，构造函数： 
，利用导数研究函数的单调性即可证明.
试题解析：（1）f（x）的定义域为（0，+∞），其导数f'（x）=
﹣a．
①当a≤0时，f'（x）＞0，函数在（0，+∞）上是增函数；
②当a＞0时，在区间（0，
）上，f'（x）＞0；在区间（，+∞）上，f'（x）＜0．
∴f（x）在（0，）是增函数，在（，+∞）是减函数．
（2）由（1）知，当a≤0时，函数f（x）在（0，+∞）上是增函数，不可能有两个零点，
当a＞0时，f（x）在（0，）上是增函数，在（
，+∞）上是减函数，此时f（）为函数f（x）的最大值，
当f（）≤0时，f（x）最多有一个零点，∴f（）=ln＞0，解得0＜a＜1，
此时，
＜
，且f（
）=﹣1﹣
+1=﹣＜0，
f（
）=2﹣2lna﹣
+1=3﹣2lna﹣（0＜a＜1），
令F（a）=3﹣2lna﹣，则F'（x）=﹣
=
＞0，∴F（a）在（0，1）上单调递增，∴F（a）＜F（1）=3﹣e2＜0，即f（）＜0，
∴a的取值范围是（0，1）．
（3）由（2）可知函数f（x）在（0，
）是增函数，在（，+∞）是减函数．分析：∵0
，∴
．只要证明：f（
）＞0就可以得出结论．
下面给出证明：构造函数：g（x）=f（
﹣x）﹣f（x）=ln（﹣x）﹣a（﹣x）﹣（lnx﹣ax）（0＜x≤
），则g'（x）=
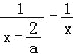+2a=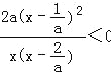
，
函数g（x）在区间（0，
]上为减函数．0＜x1
，则g（x1）＞g（）=0，又f（x1）=0，
于是f（
）=ln（）﹣a（）+1﹣f（x1）=g（x1）＞0．又f（x2）=0，
由（1）可知
，即
．
【方法点晴】本题主要考查的是利用导数研究函数的单调性、利用导数研究函数的零点、证明不等式，属于难题．利用导数研究函数
的单调性的步骤：①确定函数
的定义域；②对
求导；③令
，在定义域内解不等式得
的范围就是递增区间；令
，在定义域内解不等式得
的范围就是递减区间.
