题目内容
已知椭圆C过点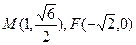 是椭圆的左焦点,P、Q是椭圆C上的两个动点,且|PF|、|MF|、|QF|成等差数列。
是椭圆的左焦点,P、Q是椭圆C上的两个动点,且|PF|、|MF|、|QF|成等差数列。
(1)求椭圆C的标准方程;
(2)求证:线段PQ的垂直平分线经过一个定点A;
(3)设点A关于原点O的对称点是B,求|PB|的最小值及相应点P的坐标。
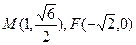 是椭圆的左焦点,P、Q是椭圆C上的两个动点,且|PF|、|MF|、|QF|成等差数列。
是椭圆的左焦点,P、Q是椭圆C上的两个动点,且|PF|、|MF|、|QF|成等差数列。(1)求椭圆C的标准方程;
(2)求证:线段PQ的垂直平分线经过一个定点A;
(3)设点A关于原点O的对称点是B,求|PB|的最小值及相应点P的坐标。
(1)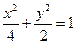 (2)
(2)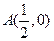 (3)
(3)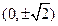
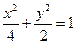 (2)
(2)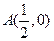 (3)
(3)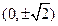
(1)设椭圆 的方程为
的方程为 ,由已知,得
,由已知,得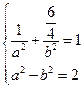 ,解得
,解得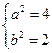
所以椭圆的标准方程为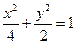 …………3分
…………3分
(2)证明:设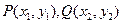 。由椭圆的标准方程为
。由椭圆的标准方程为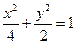 ,可知
,可知
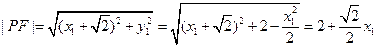
同理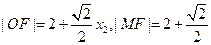 ………4分
………4分
∵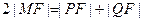 ,∴
,∴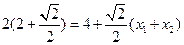
∴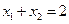 …………5分
…………5分
①当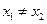 时,由
时,由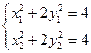 ,得
,得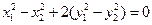
从而有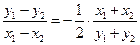
设线段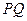 的中点为
的中点为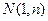 ,由
,由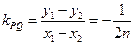 …………6分
…………6分
得线段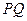 的中垂线方程为
的中垂线方程为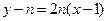 …………7分
…………7分
∴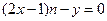 ,该直线恒过一定点
,该直线恒过一定点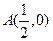 …………8分
…………8分
②当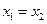 时,
时,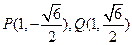 或
或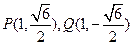
线段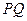 的中垂线是
的中垂线是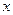 轴,也过点
轴,也过点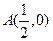 ,
,
∴线段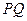 的中垂线过点
的中垂线过点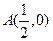 …………10分
…………10分
(3)由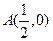 ,得
,得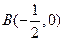 。
。
又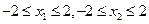 ,∴
,∴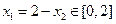
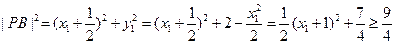 …………12分
…………12分
∴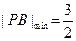 时,点
时,点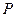 的坐标为
的坐标为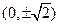 …………14分
…………14分
 的方程为
的方程为 ,由已知,得
,由已知,得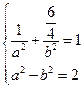 ,解得
,解得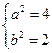
所以椭圆的标准方程为
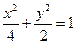 …………3分
…………3分(2)证明:设
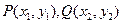 。由椭圆的标准方程为
。由椭圆的标准方程为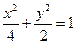 ,可知
,可知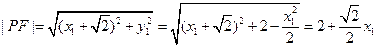
同理
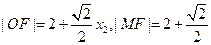 ………4分
………4分∵
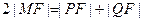 ,∴
,∴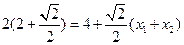
∴
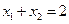 …………5分
…………5分①当
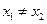 时,由
时,由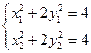 ,得
,得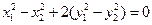
从而有
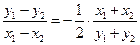
设线段
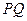 的中点为
的中点为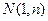 ,由
,由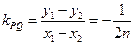 …………6分
…………6分得线段
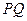 的中垂线方程为
的中垂线方程为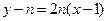 …………7分
…………7分∴
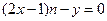 ,该直线恒过一定点
,该直线恒过一定点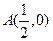 …………8分
…………8分②当
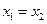 时,
时,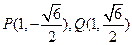 或
或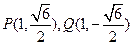
线段
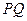 的中垂线是
的中垂线是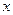 轴,也过点
轴,也过点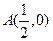 ,
,∴线段
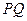 的中垂线过点
的中垂线过点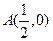 …………10分
…………10分(3)由
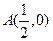 ,得
,得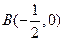 。
。又
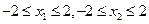 ,∴
,∴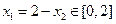
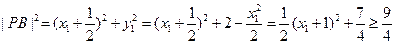 …………12分
…………12分∴
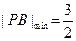 时,点
时,点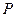 的坐标为
的坐标为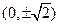 …………14分
…………14分
练习册系列答案
相关题目
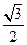 ,过点
,过点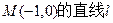 与椭圆交于
与椭圆交于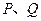 两点.
两点.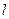 的斜率为1,且
的斜率为1,且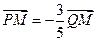 ,求椭圆的标准方程;
,求椭圆的标准方程;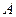 ,直线
,直线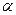 ,问
,问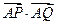 取得最大值,并求出这个最大值.
取得最大值,并求出这个最大值.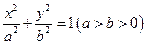 的中心在坐标原点
的中心在坐标原点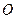 ,一条准线的方程为
,一条准线的方程为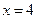 ,过椭圆的左焦点
,过椭圆的左焦点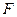 ,且方向向量为
,且方向向量为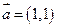 的直线
的直线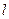 交椭圆于
交椭圆于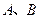 两点,
两点,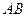 的中点为
的中点为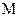
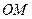 的斜率(用
的斜率(用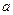 、
、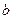 表示);
表示);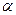 ,当
,当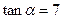 时,求椭圆的方程.
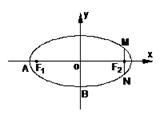
时,求椭圆的方程. 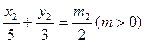 ,经过椭圆C的右焦点F且斜率为k(k≠0)的直线l交椭圆G于A、B两点,M为线段AB的中点,设O为椭圆的中心,射线OM交椭圆于N点.
,经过椭圆C的右焦点F且斜率为k(k≠0)的直线l交椭圆G于A、B两点,M为线段AB的中点,设O为椭圆的中心,射线OM交椭圆于N点.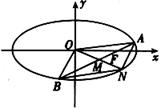
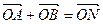 成立?若存在,求出所有k的值;
成立?若存在,求出所有k的值;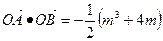 ,求实数k的取值范围.
,求实数k的取值范围.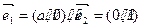 ,经过定点
,经过定点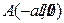 且方向向量为
且方向向量为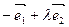 的直线与经过定点
的直线与经过定点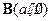 且方向向量为
且方向向量为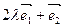 的直线交于点M,其中
的直线交于点M,其中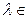 R,常数a>0.
R,常数a>0.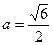 ,过点
,过点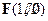 的直线与点M的轨迹交于C、D两点,求
的直线与点M的轨迹交于C、D两点,求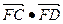 的取值范围.
的取值范围. 中,已知椭圆
中,已知椭圆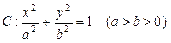 的离心率e=
的离心率e=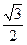 ,左右两个焦分别为
,左右两个焦分别为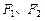 .过右焦点
.过右焦点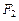 且与
且与 轴垂直的
轴垂直的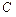 相交M、N两点,且|MN|=1.
相交M、N两点,且|MN|=1.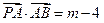 ,
,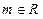 )试求点P的轨迹方程,使点B关于该轨迹的对称点落在椭圆
)试求点P的轨迹方程,使点B关于该轨迹的对称点落在椭圆
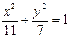 上一点到直线
上一点到直线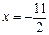 与到点(-2,0)的距离之比为
与到点(-2,0)的距离之比为  经过点
经过点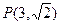 ,且与
,且与 轴交于
轴交于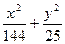 =1有两个公共点,则m的取值范围是( )
=1有两个公共点,则m的取值范围是( )