题目内容
如图,正三棱柱ABC—A1B1C1的各棱长都相等,M、E分别是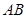 和AB1的中点,点F在BC上且满足BF∶FC=1∶3.
和AB1的中点,点F在BC上且满足BF∶FC=1∶3.
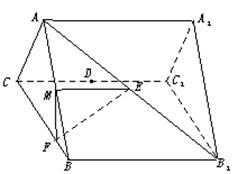
(1)求证:BB1∥平面EFM;
(2)求四面体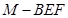 的体积.
的体积.
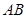 和AB1的中点,点F在BC上且满足BF∶FC=1∶3.
和AB1的中点,点F在BC上且满足BF∶FC=1∶3.
(1)求证:BB1∥平面EFM;
(2)求四面体
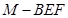 的体积.
的体积.(1)见解析;(2)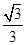 .
.
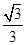 .
.试题分析:(1)要证线面平行,一般是在平面内找(证)一条直线与待证直线平行,然后由线面平行的判定定理可得结论,本题中平行线很容易找到,因为
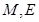 都是相应线段上的中点,因此显然有
都是相应线段上的中点,因此显然有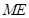 ∥
∥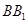 .(2)三棱锥的体积公式是
.(2)三棱锥的体积公式是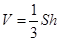 ,由于三梭锥的四个面都是三角形,故我们可以恰当地选取底面,以使得高易求(即熟知的换底法),本题中三梭锥
,由于三梭锥的四个面都是三角形,故我们可以恰当地选取底面,以使得高易求(即熟知的换底法),本题中三梭锥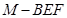 ,我们就可以以
,我们就可以以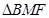 为底,而这时高就是
为底,而这时高就是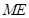 ,而高
,而高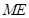 的垂直的证明可由正三梭锥的定义证得.
的垂直的证明可由正三梭锥的定义证得.试题解析:(1)证明:连结EM、MF,∵M、E分别是正三棱柱的棱AB和AB1的中点,
∴BB1∥ME, 3分
又BB1
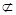 平面EFM,∴BB1∥平面EFM. 6分
平面EFM,∴BB1∥平面EFM. 6分(2)正三棱柱中
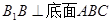 ,由(1)
,由(1)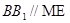 ,所以
,所以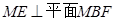 , 8分
, 8分根据条件得出
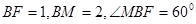 ,所以
,所以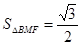 ,10分
,10分又
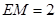 ,因此
,因此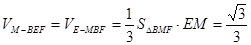 . 12分
. 12分
练习册系列答案
 作业辅导系列答案
作业辅导系列答案 同步学典一课多练系列答案
同步学典一课多练系列答案 经典密卷系列答案
经典密卷系列答案
相关题目
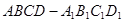 中,
中,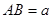 ,
,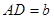 ,
,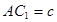 ,点
,点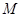 为
为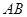 的中点,点
的中点,点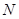 为
为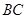 的中点.
的中点.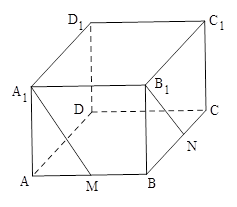
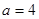 ,
,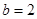 ,
,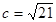 ,求异面直线
,求异面直线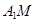 与
与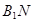 所成的角.
所成的角.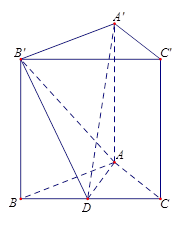
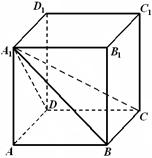
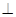 B'D;
B'D;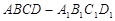 的棱长为
的棱长为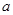 .
.
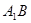 与
与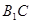 所成角的大小;
所成角的大小; 的体积.
的体积.
 中,侧棱与底面垂直,
中,侧棱与底面垂直, ,
, ,
, 分别是
分别是 的中点
的中点
 ∥平面
∥平面 ;
; ;
; 的体积.
的体积. 中,
中,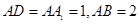 ,点E是AB的中点.
,点E是AB的中点.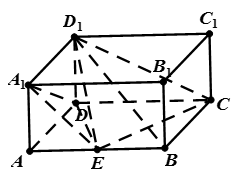
 的体积;
的体积;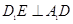 ;
; 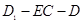 的正切值.
的正切值.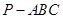 中,
中,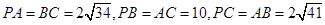 ,则三棱锥
,则三棱锥