题目内容
2.过点P(1,2)的直线l交x,y轴的正半轴与A、B两点,O为坐标原点,当|AB|最小时,直线l的方程为y-2=$\root{3}{2}$(x-1).分析 如图所示,设∠OAB=α,α∈$(0,\frac{π}{2})$.可得|PA|=$\frac{2}{sinα}$,|PB|=$\frac{1}{cosα}$.|AB|=|PA|+|PB|=$\frac{2}{sinα}$+$\frac{1}{cosα}$=f(α),利用导数研究其单调性极值即可得出.
解答 解:如图所示,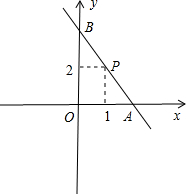
设∠OAB=α,α∈$(0,\frac{π}{2})$.
则|PA|=$\frac{2}{sinα}$,|PB|=$\frac{1}{cosα}$.
∴|AB|=|PA|+|PB|=$\frac{2}{sinα}$+$\frac{1}{cosα}$=f(α),
f′(α)=$-\frac{2cosα}{si{n}^{2}α}$+$\frac{sinα}{co{s}^{2}α}$=$\frac{(sinα-\root{3}{2}cosα)(si{n}^{2}α+\root{3}{4}cosα+\root{3}{2}sinαcosα)}{si{n}^{2}αco{s}^{2}α}$,
当tanα>$\root{3}{2}$时,f′(α)>0,此时函数f(α)单调递增;当0<tanα<$\root{3}{2}$时,f′(α)<0,此时函数f(α)单调递减.
∴当tanα=$\root{3}{2}$时,函数f(α)取得最小值,
此时直线l的方程为:y-2=$\root{3}{2}$(x-1).
故答案为:y-2=$\root{3}{2}$(x-1).
点评 本题考查了利用导数研究函数单调性极值、直线的方程、三角函数的单调性,考查了推理能力与计算能力,属于中档题.

练习册系列答案
 活力试卷系列答案
活力试卷系列答案 课课优能力培优100分系列答案
课课优能力培优100分系列答案
相关题目
10.三角形ABC中,边a=$\sqrt{6}$-$\sqrt{2}$,b=4,角C=75°,则△ABC的面积S=( )
| A. | 2 | B. | 4 | C. | 6 | D. | 2$\sqrt{6}$+2 |
14.在下列说法中,错误的是( )
| A. | 若平面α内的一条直线垂直于平面β内的任一直线,则α⊥β | |
| B. | 若平面α内任意一条直线平行于平面β,则α∥β | |
| C. | 若直线m∥平面α,直线n⊥平面β且α⊥β,则m∥n | |
| D. | 若平面α∥平面β,任取直线l?α,则l∥β |
11.正方体ABCD-A1B1C1D1中,E,F分别为棱AB,CC1的中点,在平面ADD1A1内且与平面D1EF平行的直线( )
| A. | 有无数条 | B. | 有2条 | C. | 有1条 | D. | 不存在 |
12.已知(2x3+$\frac{1}{x}$)n展开式中的常数项是第七项,则n=( )
| A. | 7 | B. | 8 | C. | 9 | D. | 10 |