题目内容
已知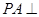 矩形ABCD所在平面,PA=AD=
矩形ABCD所在平面,PA=AD=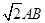 ,E为线段PD上一点,G为线段PC的中点.
,E为线段PD上一点,G为线段PC的中点.
(1)当E为PD的中点时,求证: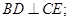
(2)当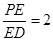 时,求证:BG//平面AEC.
时,求证:BG//平面AEC.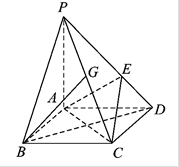
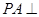 矩形ABCD所在平面,PA=AD=
矩形ABCD所在平面,PA=AD=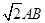 ,E为线段PD上一点,G为线段PC的中点.
,E为线段PD上一点,G为线段PC的中点.(1)当E为PD的中点时,求证:
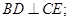
(2)当
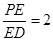 时,求证:BG//平面AEC.
时,求证:BG//平面AEC.
(1)过E作EH⊥AD,垂足为H,连接CH.
 ,
,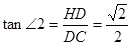 ,
,
∴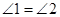
又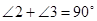 ,∴
,∴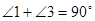 ,∴BD⊥CH,
,∴BD⊥CH,
∴BD⊥CE。 (6分)
(2)取PE的中点F,连接GF,BF。
∵G为PC的中点,
∴GF//CE
∴GF//平面ACE。连接BD交AC与点O,连接OE.
∵E为DF的中点,
∴BF//OE
∴BF//平面ACE。∵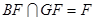 ,
,
∴平面BGF//平面AEC。
又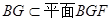 ∴BG//平面AEC……(12分)
∴BG//平面AEC……(12分)
 ,
,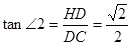 ,
,∴
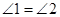
又
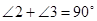 ,∴
,∴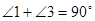 ,∴BD⊥CH,
,∴BD⊥CH,∴BD⊥CE。 (6分)
(2)取PE的中点F,连接GF,BF。
∵G为PC的中点,
∴GF//CE
∴GF//平面ACE。连接BD交AC与点O,连接OE.
∵E为DF的中点,
∴BF//OE
∴BF//平面ACE。∵
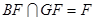 ,
,∴平面BGF//平面AEC。
又
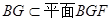 ∴BG//平面AEC……(12分)
∴BG//平面AEC……(12分)略

练习册系列答案
相关题目
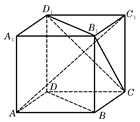
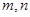 是两条不同的直线,
是两条不同的直线,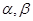 是两个不同的平面,则下列命题中的假命题是
是两个不同的平面,则下列命题中的假命题是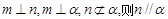
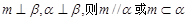
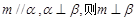
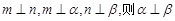
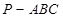 中,
中,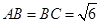 ,平面
,平面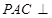 平面
平面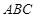 ,
,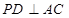 于点
于点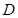 ,
, 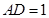 ,
,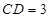 ,
,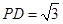 .
.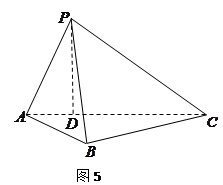
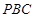 为直角三角形;
为直角三角形;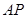 与平面
与平面 中,
中,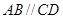 ,
,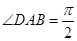 ,点
,点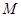 、
、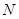 分别在
分别在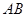 ,
,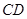 上,且
上,且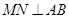 ,
,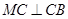 ,
, ,
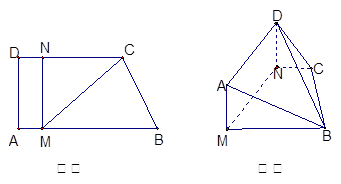
,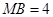 ,现将梯形
,现将梯形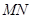 折起,使平面
折起,使平面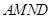 与平面
与平面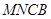 垂直(如图乙).
垂直(如图乙).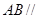 平面
平面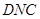 ;
;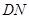 的长为何值时,二面角
的长为何值时,二面角 的大小为
的大小为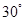 ?
?
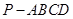 的底面
的底面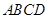 为菱形,且
为菱形,且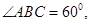
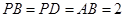 ,
,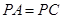 ,
,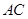 与
与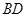 相交于点
相交于点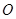 .
.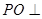 底面
底面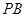 与平面
与平面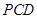 所成角的正弦值;
所成角的正弦值;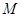 是
是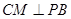 ,求
,求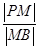 的值.
的值.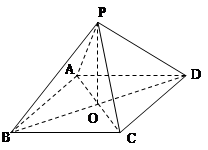
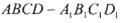 棱长为1,点
棱长为1,点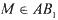 ,
,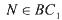 ,且
,且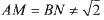 ,有以下四个结论:
,有以下四个结论: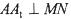 ,②
,②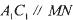 ;③.
;③.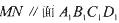 ;④MN与
;④MN与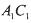 是异面直线、其中正确结论的序号是________ (注:把你认为正确命题的序号都填上)
是异面直线、其中正确结论的序号是________ (注:把你认为正确命题的序号都填上)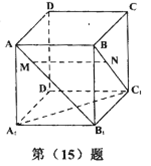
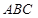 为底面的直棱柱
为底面的直棱柱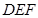 所截而得.
所截而得. 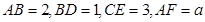 ,
,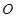 为
为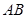 的中点.
的中点.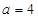 时,求平面
时,求平面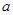 为何值时,在棱
为何值时,在棱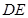 上存在点
上存在点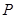 ,使
,使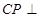 平面
平面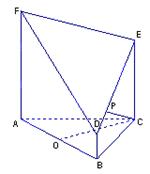
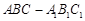 ,
,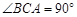 ,
,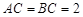 ,
,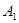 在底面
在底面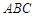 上的射影恰为
上的射影恰为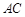 的中点
的中点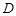 ,又知
,又知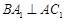 .
.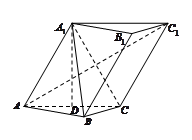
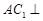 平面
平面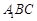 ;
; 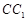 到平面
到平面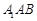 的距离;
的距离;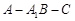 的大小。
的大小。