题目内容
一般地,给定平面上有n个点,每两点之间有一个距离,最大距离与最小距离的比记为λn,已知λ4的最小值是
,λ5的最小值是2sin
π,λ6的最小值是
.试猜想λn(n≥4)的最小值是______.(这就是著名的Heilbron猜想,已经被我国的数学家攻克)
| 2 |
| 3 |
| 10 |
| 3 |
∵λ4=
=2sin
,
λ5=2sin
π,
λ6=
=2sin
,
…
设数列{an}(n≥4),a4=
=
-
,a5=
=
-
,a6=
-
,…
于是可得an=
-
.
∴猜想λn(n≥4)的最小值是2sin(
-
)π=2sin
π.
故答案为2sin
π.
| 2 |
| π |
| 4 |
λ5=2sin
| 3 |
| 10 |
λ6=
| 3 |
| π |
| 3 |
…
设数列{an}(n≥4),a4=
| 1 |
| 4 |
| 1 |
| 2 |
| 1 |
| 4 |
| 3 |
| 10 |
| 1 |
| 2 |
| 1 |
| 5 |
| 1 |
| 2 |
| 1 |
| 6 |
于是可得an=
| 1 |
| 2 |
| 1 |
| n |
∴猜想λn(n≥4)的最小值是2sin(
| 1 |
| 2 |
| 1 |
| n |
| n-2 |
| 2n |
故答案为2sin
| n-2 |
| 2n |

练习册系列答案
相关题目
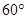 ;
;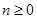 ,试用分析法证明:
,试用分析法证明: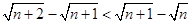 .
. 的前
的前 项和为
项和为 ,则
,则 ,
, ,
, ,
, 成等差数列.类比
成等差数列.类比 的前
的前 ,则
,则 , ,
, , 成等比数列.
成等比数列.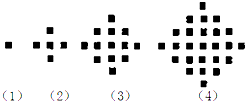
 内( )
内( ) ,其中
,其中 为常数,等号右边的运算是通常意义的加乘运算,现已知
为常数,等号右边的运算是通常意义的加乘运算,现已知 ,
, ,且有一个非零实数m,使得对任意实数x,都有
,且有一个非零实数m,使得对任意实数x,都有 ,则
,则 ______________。
______________。 ,
, ,推测当
,推测当 时,有_____.
时,有_____.