题目内容
类比平面内直角三角形的勾股定理，在空间四面体P-ABC中，记底面△ABC的面积为S0，三个侧面的面积分别为S1，S2，S3，若PA，PB，PC两两垂直，则有结论______．
设三个侧棱是a，b，c，则三个侧面的面积分别是
，
，
．
三条底边的长为
，
，
，
由余弦定理，可得底面的面积是
∵底面△ABC的面积为S0，三个侧面的面积分别为S1，S2，S3，
∴
=
+
+
故答案为：
=
+
+
| ab |
| 2 |
| bc |
| 2 |
| ac |
| 2 |
三条底边的长为
| a2+b2 |
| b2+c2 |
| a2+c2 |
由余弦定理，可得底面的面积是
| ||
| 2 |
∵底面△ABC的面积为S0，三个侧面的面积分别为S1，S2，S3，
∴
| S | 20 |
| S | 21 |
| S | 22 |
| S | 23 |
故答案为：
| S | 20 |
| S | 21 |
| S | 22 |
| S | 23 |
练习册系列答案
同步学典一课多练系列答案
经典密卷系列答案
金牌课堂练系列答案
相关题目
、
，运算“
”、“
”定义为：
=
，
=
，则下列各式其中恒成立的是（ 
）
⑵
⑷
，
是
的小数部分，则当
时，
的值（ ）．
、必为无理数；
、必为偶数；
、必为奇数；
、可为无理数或有理数．
(
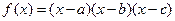是两两不等的常数),则
的值是 ______________.