题目内容
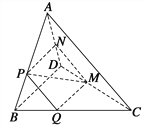
【题目】如图,在四棱锥![]() 中,底面
中,底面![]() 是菱形,
是菱形,![]() ,侧面
,侧面![]() 是边长为2的等边三角形,点
是边长为2的等边三角形,点![]() 是
是![]() 的中点,且平面
的中点,且平面![]() 平面
平面![]() .
.
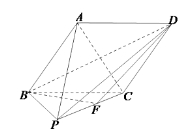
(I)求异面直线![]() 与
与![]() 所成角的余弦值;
所成角的余弦值;
(II)若点![]() 在线段
在线段![]() 上移动,是否存在点
上移动,是否存在点![]() 使平面
使平面![]() 与平面
与平面![]() 所成的角为
所成的角为![]() ?若存在,指出点
?若存在,指出点![]() 的位置,否则说明理由.
的位置,否则说明理由.
【答案】(I)![]() ;(II)不存在,理由见解析.
;(II)不存在,理由见解析.
【解析】
试题分析:根据题设条件取![]() 中点
中点![]() ,以
,以![]() 为坐标原点,
为坐标原点,![]() 为
为![]() 轴,
轴,![]() 为
为![]() 轴建立空间直角坐标系.(I)利用向量法可求得异面直线
轴建立空间直角坐标系.(I)利用向量法可求得异面直线![]() 与
与![]() 所成角的余弦值.(II)首先设存在
所成角的余弦值.(II)首先设存在![]() 点,且
点,且![]() ,根据
,根据![]() 三点共线,利用向量法求得
三点共线,利用向量法求得![]() 点,然后利用面面角为直角,由法向量构建方程,可求得
点,然后利用面面角为直角,由法向量构建方程,可求得![]() 不符合题意,所以不存在.
不符合题意,所以不存在.
试题解析:(I)因为平面![]() 平面
平面![]() ,底面
,底面![]() 是菱形,
是菱形,![]() ,
,
故![]() ,取
,取![]() 中点
中点![]() ,则
,则![]() ,
,![]() ,
,![]() .
.
以![]() 为坐标原点,
为坐标原点,![]() 为
为![]() 轴,
轴,![]() 为
为![]() 轴建立平面直角坐标系
轴建立平面直角坐标系![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() .………………2分
.………………2分
![]() ,
,![]() ,
,
则![]() ,
,![]() ,
,![]() .
.
设异面直线![]() 与
与![]() 所成角为
所成角为![]() ,
,![]() ,
,
所以异面直线![]() 与
与![]() 所成角的余弦值为
所成角的余弦值为![]() .………………6分
.………………6分

(II)设存在点![]() ,使平面
,使平面![]() 与平面
与平面![]() 所成的角为
所成的角为![]() ,
,
设![]() ,因为
,因为![]() 三点共线,
三点共线,![]() ,
,![]() ,
,![]() ,
,
所以![]() ,
,![]() ,
,![]() ,
,
设平面![]() 的一个法向量为
的一个法向量为![]() ,
,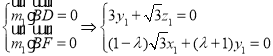 ,
,
令![]() ,
,![]() ,
,![]() .………………8分
.………………8分
设平面![]() 的一个法向量为
的一个法向量为![]() ,
,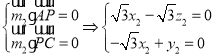 ,
,
令![]() ,
,![]() ,
,![]() ,又
,又![]() .………………10分
.………………10分
若平面![]() 与平面
与平面![]() 所成的角为
所成的角为![]() ,则
,则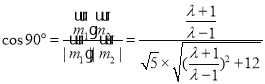 ,
,
故![]() ,即
,即![]() ,此时
,此时![]() ,点
,点![]() 在
在![]() 延长线上,
延长线上,
所以在![]() 边上不存在点
边上不存在点![]() 使平面
使平面![]() 与平面
与平面![]() 所成的角为
所成的角为![]() .………………12分
.………………12分

 阅读快车系列答案
阅读快车系列答案【题目】在一次篮球定点投篮训练中,规定每人最多投3次,在![]() 处每投进一球得3分;在
处每投进一球得3分;在![]() 处每投进一球得2分,如果前两次得分之和超过3分就停止投篮;否则投第3次,某同学在
处每投进一球得2分,如果前两次得分之和超过3分就停止投篮;否则投第3次,某同学在![]() 处的抽中率
处的抽中率![]() ,在
,在![]() 处的抽中率为
处的抽中率为![]() ,该同学选择现在
,该同学选择现在![]() 处投第一球,以后都在
处投第一球,以后都在![]() 处投,且每次投篮都互不影响,用
处投,且每次投篮都互不影响,用![]() 表示该同学投篮训练结束后所得的总分,其分布列为:
表示该同学投篮训练结束后所得的总分,其分布列为:
| 0 | 2 | 3 | 4 | 5 |
| 0.03 |
|
|
|
|
(1)求![]() 的值;
的值;
(2)求随机变量![]() 的数学期望
的数学期望![]() ;
;
(3)试比较该同学选择上述方式投篮得分超过3分与选择都在![]() 处投篮得分超过3分的概率的大小.
处投篮得分超过3分的概率的大小.