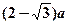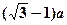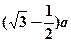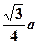题目内容
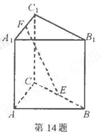
(本小题满分12分) 如图,AB是⊙O的直径,PA垂直于⊙O所在的平面,C是圆周上不同于A,B的一点.
(1)证明:平面PAC⊥平面PBC;
 (2)若
(2)若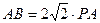 ,∠ABC=30°,求二面角A—PB—C的大小.
,∠ABC=30°,求二面角A—PB—C的大小.
(1)证明:平面PAC⊥平面PBC;
 (2)若
(2)若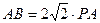 ,∠ABC=30°,求二面角A—PB—C的大小.
,∠ABC=30°,求二面角A—PB—C的大小.(1)平面PAC⊥平面PBC
(2)二面角A—PB—C的大小为60°
(2)二面角A—PB—C的大小为60°
(1)证明:∵PA垂直于⊙O所在的平面,BC在该平面内,所以PA⊥BC。
∵C是圆周上不同于A,B的一点,AB是⊙O的直径,所以∠BCA是直角,即BC⊥AC。
又因为PA与AC是平面PAC内的两条相交直线,所以BC⊥平面PAC。
又困为BC在平面PBC内,所以平面PAC⊥平面PBC …………………5分
(2)作AD⊥PB于D点,AE⊥PC于E点,连DE。
由(1)知平面PAC⊥平面PBC,所以AE⊥平面PBC
而PB在平面PBC内,所以AE⊥PB
即有PB⊥AD(所作)PB⊥AE,又AE与AD是平面ADE内的两条相交直线,
所以PB⊥平面ADE,所以∠ADE是二面角A—PB—C的平面角。…………………………9分
 设AB=2r,在Rt△ABC中,∠ABC=30°,所以AC=r
设AB=2r,在Rt△ABC中,∠ABC=30°,所以AC=r
由条件知PA=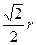
在Rt△PAC中,AE=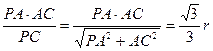
在Rt△PAB中,AD=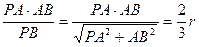
在Rt△AED中,sin∠ADE=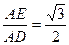 ,所以∠ADE=60°
,所以∠ADE=60°
故二面角A—PB—C的大小为60°………………………………………12分
∵C是圆周上不同于A,B的一点,AB是⊙O的直径,所以∠BCA是直角,即BC⊥AC。
又因为PA与AC是平面PAC内的两条相交直线,所以BC⊥平面PAC。
又困为BC在平面PBC内,所以平面PAC⊥平面PBC …………………5分
(2)作AD⊥PB于D点,AE⊥PC于E点,连DE。
由(1)知平面PAC⊥平面PBC,所以AE⊥平面PBC
而PB在平面PBC内,所以AE⊥PB
即有PB⊥AD(所作)PB⊥AE,又AE与AD是平面ADE内的两条相交直线,
所以PB⊥平面ADE,所以∠ADE是二面角A—PB—C的平面角。…………………………9分
 设AB=2r,在Rt△ABC中,∠ABC=30°,所以AC=r
设AB=2r,在Rt△ABC中,∠ABC=30°,所以AC=r由条件知PA=
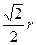
在Rt△PAC中,AE=
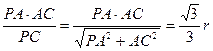
在Rt△PAB中,AD=
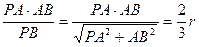
在Rt△AED中,sin∠ADE=
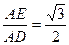 ,所以∠ADE=60°
,所以∠ADE=60°故二面角A—PB—C的大小为60°………………………………………12分

练习册系列答案
相关题目

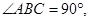
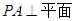 ,
,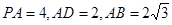 ,BC=6.
,BC=6.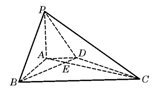
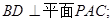
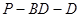 的大小.
的大小.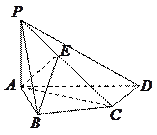
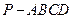 中,
中,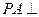 底面
底面 ,
,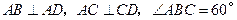 ,
,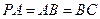 ,
,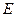 是
是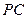 的中点.
的中点.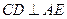 ;
;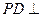 平面
平面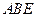 ;
;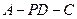 的大小.
的大小.
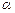 ,直线
,直线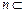 平面
平面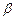 ,则下列命题正确的是 ( )
,则下列命题正确的是 ( )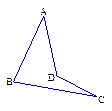
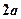 的正方体容器被水充满,首先把半径为
的正方体容器被水充满,首先把半径为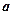 的球放入其中,再放入一个能被水完全淹没的小球,若想使溢出的水量最大,这个小球的半径为( )
的球放入其中,再放入一个能被水完全淹没的小球,若想使溢出的水量最大,这个小球的半径为( )