题目内容
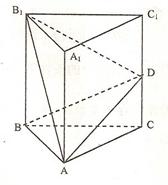
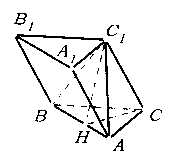
(本小题满分15分)如图,斜三棱柱ABC—A1B1C1中,A1C1⊥BC1,AB⊥AC,AB=3,AC=2,侧棱与底面成60°角.
(1)求证:AC⊥面ABC1;
(2)求证:C1点在平面ABC上的射影H在直线AB上;
(3)求此三棱柱体积的最小值.
(1)求证:AC⊥面ABC1;
(2)求证:C1点在平面ABC上的射影H在直线AB上;
(3)求此三棱柱体积的最小值.

(1)由棱柱性质,可知A1C1//AC,∵A1C1 BC1,
BC1,
∴AC BC1,又∵AC
BC1,又∵AC AB,∴AC
AB,∴AC 平面ABC1
平面ABC1
(2)由(1)知AC 平面ABC1,又AC
平面ABC1,又AC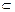 平面ABC,∴平面ABC
平面ABC,∴平面ABC 平面ABC1,
平面ABC1,
在平面ABC1内,过C1作C1H AB于H,则C1H
AB于H,则C1H 平面ABC,故点C1在平面ABC上
平面ABC,故点C1在平面ABC上
的射影H在直线AB上.
(3)3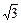
 .
.
 BC1,
BC1, ∴AC
 BC1,又∵AC
BC1,又∵AC AB,∴AC
AB,∴AC 平面ABC1
平面ABC1(2)由(1)知AC
 平面ABC1,又AC
平面ABC1,又AC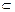 平面ABC,∴平面ABC
平面ABC,∴平面ABC 平面ABC1,
平面ABC1,在平面ABC1内,过C1作C1H
 AB于H,则C1H
AB于H,则C1H 平面ABC,故点C1在平面ABC上
平面ABC,故点C1在平面ABC上的射影H在直线AB上.
(3)3
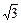
 .
.
(1)由棱柱性质,可知A1C1//AC,∵A1C1
 BC1,
BC1, ∴AC
 BC1,又∵AC
BC1,又∵AC AB,∴AC
AB,∴AC 平面ABC1
平面ABC1(2)由(1)知AC
 平面ABC1,又AC
平面ABC1,又AC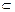 平面ABC,∴平面ABC
平面ABC,∴平面ABC 平面ABC1,
平面ABC1,在平面ABC1内,过C1作C1H
 AB于H,则C1H
AB于H,则C1H 平面ABC,故点C1在平面ABC上
平面ABC,故点C1在平面ABC上的射影H在直线AB上.
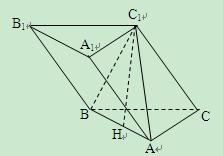
(3)连结HC,由(2)知C1H
 平面ABC, ∴∠C1CH就是侧棱CC1与底面所成的角,
平面ABC, ∴∠C1CH就是侧棱CC1与底面所成的角,∴∠C1CH=60°,C1H=CH·tan60°=
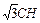
V棱柱=
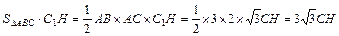
∵CA
 AB,∴CH
AB,∴CH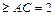 ,所以棱柱体积最小值3
,所以棱柱体积最小值3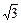
 .
.
练习册系列答案
 新活力总动员暑系列答案
新活力总动员暑系列答案 龙人图书快乐假期暑假作业郑州大学出版社系列答案
龙人图书快乐假期暑假作业郑州大学出版社系列答案
相关题目
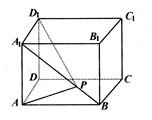
 (2)若
(2)若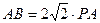 ,∠ABC=30°,求二面角A—PB—C的大小.
,∠ABC=30°,求二面角A—PB—C的大小.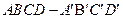 的棱长为1,点
的棱长为1,点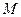 是棱
是棱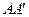 的中点,点
的中点,点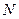 是棱
是棱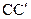 的中点,点
的中点,点 是上底面
是上底面 的中心.
的中心.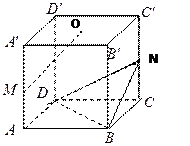 (Ⅰ)求证:MO∥平面NBD;
(Ⅰ)求证:MO∥平面NBD;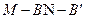 的大小;
的大小;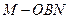 的体积.
的体积.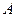 、
、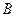 、
、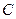 是展
是展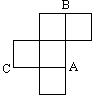
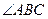 的值为
的值为 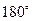

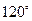
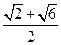
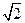
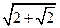
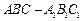 中,
中,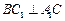 .有下列条件:
.有下列条件: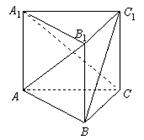
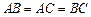 ;②
;②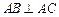 ;③
;③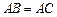 .其中能成为
.其中能成为 的充要条件的是(填上该条件的序号)________。
的充要条件的是(填上该条件的序号)________。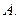 平行
平行 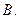 垂直
垂直 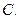 相交
相交 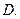 异面
异面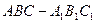 各条棱长均为1,D是侧棱
各条棱长均为1,D是侧棱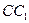 中点。
中点。