题目内容
已知直线m⊥平面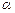 ,直线
,直线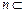 平面
平面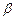 ,则下列命题正确的是 ( )
,则下列命题正确的是 ( )
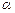 ,直线
,直线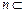 平面
平面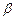 ,则下列命题正确的是 ( )
,则下列命题正确的是 ( )| A.若α∥β,则m⊥n | B.若α⊥β,则m∥n |
| C.若m⊥n,则α∥β | D.若n∥α,则α∥β |
A
略

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
题目内容
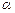 ,直线
,直线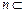 平面
平面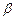 ,则下列命题正确的是 ( )
,则下列命题正确的是 ( )| A.若α∥β,则m⊥n | B.若α⊥β,则m∥n |
| C.若m⊥n,则α∥β | D.若n∥α,则α∥β |

 阅读快车系列答案
阅读快车系列答案