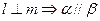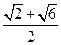题目内容
(本小题满分12分)
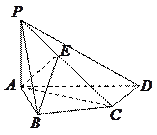
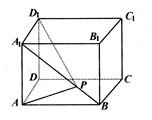
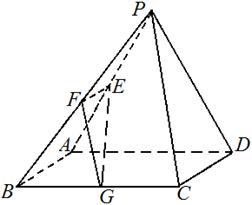
如图,在四棱锥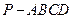 中,
中,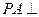 底面
底面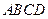 ,
,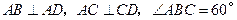 ,
,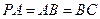 ,
,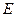 是
是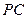 的中点.
的中点.
(Ⅰ)证明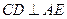 ;
;
(Ⅱ)证明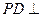 平面
平面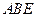 ;
;
(Ⅲ)求二面角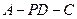 的大小.
的大小.
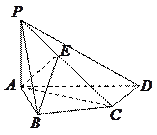
如图,在四棱锥
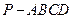 中,
中,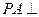 底面
底面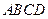 ,
,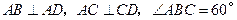 ,
,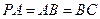 ,
,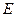 是
是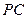 的中点.
的中点.(Ⅰ)证明
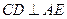 ;
;(Ⅱ)证明
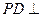 平面
平面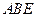 ;
;(Ⅲ)求二面角
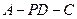 的大小.
的大小.(Ⅰ)证明:在四棱锥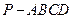 中,因
中,因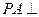 底面
底面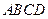 ,
,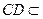 平面
平面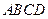 ,故
,故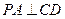 .
.
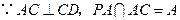 ,
,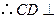 平面
平面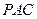 .
.
而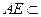 平面
平面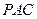 ,
,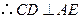 .
.
(Ⅱ)证明:由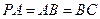 ,
,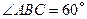 ,可得
,可得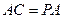 .
.
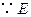 是
是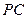 的中点,
的中点,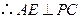 .
.
由(Ⅰ)知,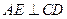 ,且
,且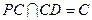 ,所以
,所以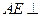 平面
平面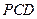 .
.
而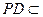 平面
平面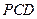 ,
,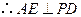 .
.
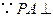 底面
底面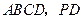 在底面
在底面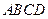 内的射影是
内的射影是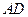 ,
,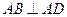 ,
,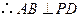 .
.
又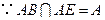 ,综上得
,综上得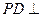 平面
平面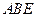 .
.
(Ⅲ)二面角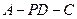 的大小是
的大小是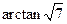
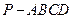 中,因
中,因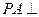 底面
底面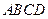 ,
,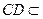 平面
平面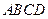 ,故
,故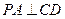 .
.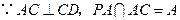 ,
,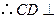 平面
平面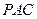 .
.而
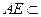 平面
平面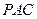 ,
,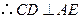 .
.(Ⅱ)证明:由
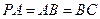 ,
,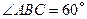 ,可得
,可得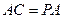 .
.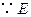 是
是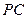 的中点,
的中点,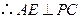 .
.由(Ⅰ)知,
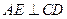 ,且
,且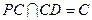 ,所以
,所以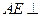 平面
平面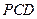 .
.而
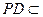 平面
平面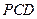 ,
,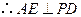 .
.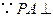 底面
底面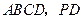 在底面
在底面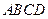 内的射影是
内的射影是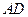 ,
,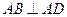 ,
,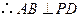 .
.又
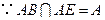 ,综上得
,综上得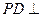 平面
平面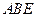 .
.(Ⅲ)二面角
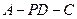 的大小是
的大小是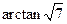
(Ⅰ)证明:在四棱锥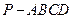 中,因
中,因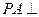 底面
底面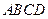 ,
,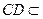 平面
平面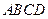 ,故
,故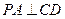 .
.
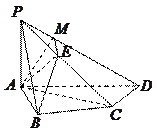
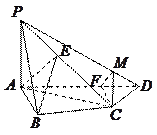
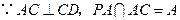 ,
,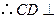 平面
平面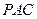 .
.
而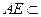 平面
平面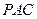 ,
,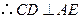 .
.
(Ⅱ)证明:由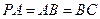 ,
,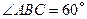 ,可得
,可得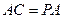 .
.
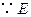 是
是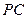 的中点,
的中点,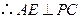 .
.
由(Ⅰ)知,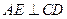 ,且
,且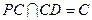 ,所以
,所以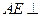 平面
平面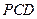 .
.
而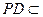 平面
平面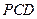 ,
,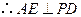 .
.
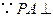 底面
底面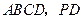 在底面
在底面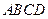 内的射影是
内的射影是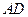 ,
,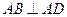 ,
,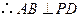 .
.
又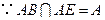 ,综上得
,综上得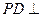 平面
平面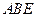 .
.
(Ⅲ)解法一:过点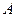 作
作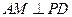 ,垂足为
,垂足为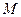 ,连结
,连结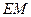 .则(Ⅱ)知,
.则(Ⅱ)知,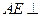 平面
平面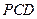 ,
,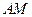 在平面
在平面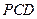 内的射影是
内的射影是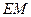 ,则
,则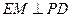 .
.
因此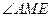 是二面角
是二面角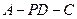 的平面角.
的平面角.
由已知,得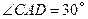 .设
.设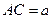 ,
,
可得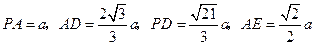 .
.
在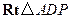 中,
中,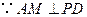 ,
,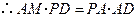 ,
,
则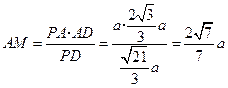 .
.
在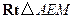 中,
中,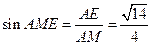 .
.
所以二面角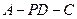 的大小是
的大小是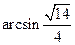 .
.
解法二:由题设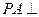 底面
底面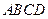 ,
,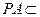 平面
平面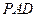 ,则平面
,则平面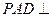 平面
平面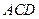 ,交线为
,交线为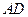 .
.
过点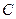 作
作 ,垂足为
,垂足为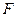 ,故
,故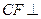 平面
平面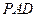 .过点
.过点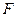 作
作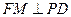 ,垂足为
,垂足为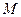 ,连结
,连结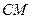 ,故
,故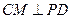 .因此
.因此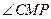 是二面角
是二面角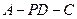 的平面角.
的平面角.
由已知,可得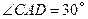 ,设
,设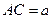 ,
,
可得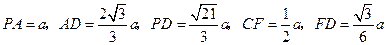 .
.
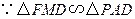 ,
,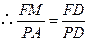 .
.
于是,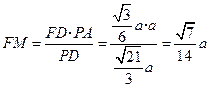 .
.
在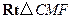 中,
中,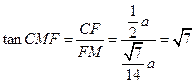 .
.
所以二面角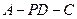 的大小是
的大小是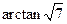 .
.
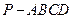 中,因
中,因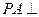 底面
底面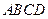 ,
,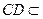 平面
平面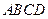 ,故
,故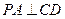 .
.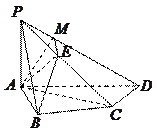
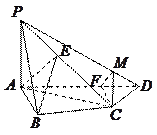
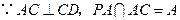 ,
,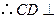 平面
平面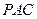 .
.而
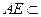 平面
平面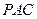 ,
,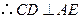 .
.(Ⅱ)证明:由
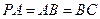 ,
,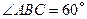 ,可得
,可得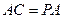 .
.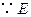 是
是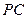 的中点,
的中点,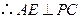 .
.由(Ⅰ)知,
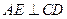 ,且
,且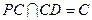 ,所以
,所以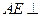 平面
平面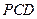 .
.而
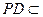 平面
平面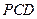 ,
,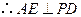 .
.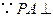 底面
底面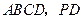 在底面
在底面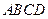 内的射影是
内的射影是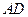 ,
,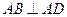 ,
,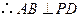 .
.又
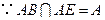 ,综上得
,综上得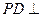 平面
平面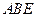 .
.(Ⅲ)解法一:过点
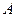 作
作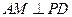 ,垂足为
,垂足为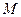 ,连结
,连结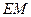 .则(Ⅱ)知,
.则(Ⅱ)知,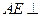 平面
平面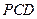 ,
,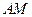 在平面
在平面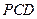 内的射影是
内的射影是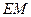 ,则
,则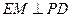 .
.因此
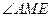 是二面角
是二面角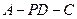 的平面角.
的平面角.由已知,得
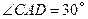 .设
.设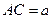 ,
,可得
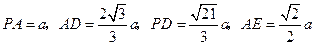 .
.在
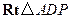 中,
中,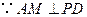 ,
,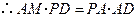 ,
,则
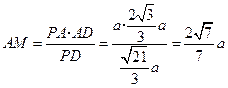 .
.在
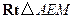 中,
中,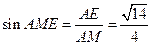 .
.所以二面角
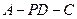 的大小是
的大小是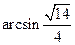 .
.解法二:由题设
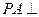 底面
底面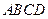 ,
,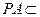 平面
平面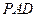 ,则平面
,则平面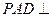 平面
平面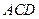 ,交线为
,交线为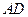 .
.过点
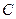 作
作 ,垂足为
,垂足为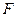 ,故
,故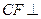 平面
平面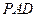 .过点
.过点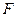 作
作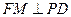 ,垂足为
,垂足为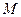 ,连结
,连结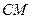 ,故
,故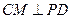 .因此
.因此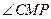 是二面角
是二面角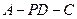 的平面角.
的平面角.由已知,可得
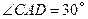 ,设
,设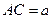 ,
,可得
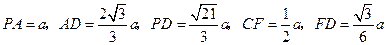 .
.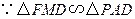 ,
,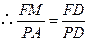 .
.于是,
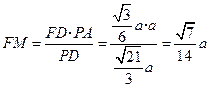 .
.在
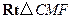 中,
中,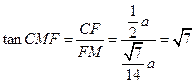 .
.所以二面角
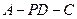 的大小是
的大小是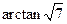 .
.
练习册系列答案
 应用题天天练四川大学出版社系列答案
应用题天天练四川大学出版社系列答案
相关题目
 平面PAD;
平面PAD; ?
?
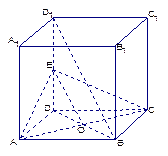
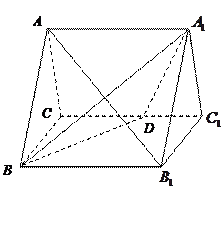 如图,正三棱柱
如图,正三棱柱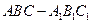 的所有棱长都为
的所有棱长都为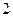 ,
,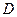 为
为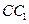 中点.
中点.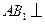 平面
平面 ;
;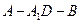 的大小;
的大小;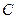 到平面
到平面 (2)若
(2)若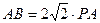 ,∠ABC=30°,求二面角A—PB—C的大小.
,∠ABC=30°,求二面角A—PB—C的大小.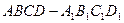 中,点
中,点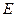 是
是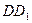 的中点.
的中点. 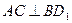 ;
;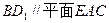 .
.
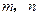 是两条不同的直线,
是两条不同的直线,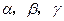 是三个不同的平面,则下列命题中的真命题是( )
是三个不同的平面,则下列命题中的真命题是( )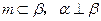 ,则
,则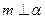
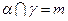
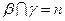 ,
,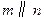 ,则
,则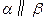
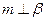 ,
,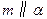 ,则
,则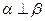
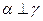 ,
,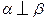 ,则
,则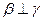
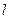 ⊥平面
⊥平面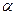 ,直线
,直线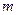
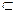 平面
平面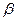 ,给出下列四个命题:
,给出下列四个命题: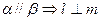 ②
②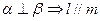 ③
③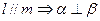 ④
④