题目内容

解法一:
根据题意有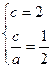 解得a = 4
解得a = 4
又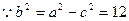
∴轨迹方程为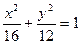
轨迹曲线是以4为半长轴、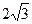 为半短轴;中心在原点,坐标轴为对称轴的椭圆。
为半短轴;中心在原点,坐标轴为对称轴的椭圆。
根据题意有
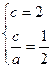 解得a = 4
解得a = 4又
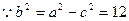
∴轨迹方程为
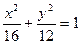
轨迹曲线是以4为半长轴、
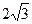 为半短轴;中心在原点,坐标轴为对称轴的椭圆。
为半短轴;中心在原点,坐标轴为对称轴的椭圆。此题的给出恰符合圆锥曲线的统一定义,又因为其比值为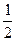 < 1。
< 1。
所以轨迹是一个椭圆。
解法二:轨迹法
设点P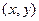 , 点P到定直线的距离为
, 点P到定直线的距离为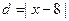
即: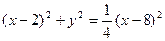
化简得: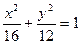 为所求方程动点P的轨迹方程。
为所求方程动点P的轨迹方程。
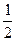 < 1。
< 1。所以轨迹是一个椭圆。
解法二:轨迹法
设点P
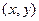 , 点P到定直线的距离为
, 点P到定直线的距离为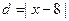
即:
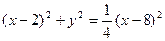
化简得:
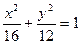 为所求方程动点P的轨迹方程。
为所求方程动点P的轨迹方程。
练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
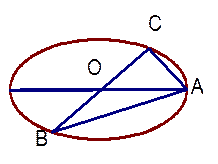
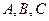 是长轴为4的椭圆上的三点,点
是长轴为4的椭圆上的三点,点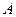 是长轴的一个顶点,
是长轴的一个顶点,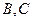 过椭圆中心
过椭圆中心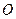 (如图),且
(如图),且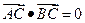 ,
,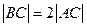
 (Ⅱ)如果椭圆上的两点
(Ⅱ)如果椭圆上的两点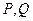 ,使
,使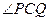 的平分线垂直于
的平分线垂直于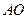 ,是否总存在实数
,是否总存在实数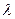 ,使
,使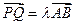 。请给出证明。
。请给出证明。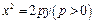 上的两个动点,
上的两个动点,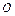 为坐标原点,非零向量
为坐标原点,非零向量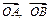 满足
满足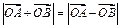 .
.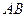 经过一定点;
经过一定点;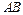 的中点到直线
的中点到直线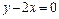 的距离的最小值为
的距离的最小值为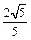 时,求
时,求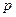 的值.
的值.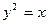
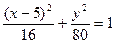
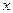
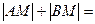
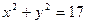
 相交于A、B两点,M是线段AB上的一点,
相交于A、B两点,M是线段AB上的一点,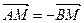 ,且点M在直线
,且点M在直线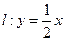 上.
上.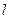 的对称点在单位圆
的对称点在单位圆 上,求椭圆的方程.
上,求椭圆的方程. :
: ,直线
,直线 交
交 两点,
两点, 是线段
是线段 的中点,过
的中点,过 轴的垂线交
轴的垂线交 .(1)证明:抛物线
.(1)证明:抛物线 使NA
使NA NB,若存在,求
NB,若存在,求
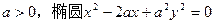
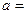
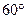 的直线被圆学
的直线被圆学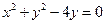 所截得的弦长为科网
所截得的弦长为科网

