题目内容
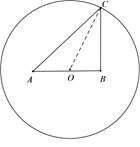
【题目】（本小题满分12分）如图所示，
是一个矩形花坛，其中
米，
米．现将矩形花坛扩建成一个更大的矩形花坛
，要求：
在
上，
在
上，对角线
过
点，且矩形的面积小于150平方米．
（1）设
长为
米，矩形的面积为
平方米，试用解析式将
表示成
的函数，并确定函数的定义域；
（2）当
的长度是多少时，矩形的面积最小？并求最小面积．
【答案】（1）
,
;（2）
,
.
【解析】
试题（1）根据三角形的相似性，列出函数关系式，通分化成标准形式，求分式不等式的解集；（2）通过换元，令
，则得到
关于
的函数，根据均值不等式，有
的最小值
.
试题解析：（1）由
可得，
，∴．
由
，且
，解得
，∴函数的定义域为
．
（2）令
，则
，
，
当且仅当
时，
取最小值
，故当
的长度为
米时，矩形花坛
的面积最小，最小面积为96平方米．
练习册系列答案
课堂全解字词句段篇章系列答案
相关题目
